
【题目】中国女排,曾经十度成为世界冠军,铸就了响彻中华的女排精神.女排精神的具体表现为:扎扎实实,勤学苦练,无所畏惧,顽强拼搏,同甘共苦,团结战斗,刻苦钻研,勇攀高峰.女排精神对各行各业的劳动者起到了激励、感召和促进作用,给予全国人民巨大的鼓舞.
(1)看过中国女排的纪录片后,某大学掀起“学习女排精神,塑造健康体魄”的年度主题活动,一段时间后,学生的身体素质明显提高,将该大学近5个月体重超重的人数进行统计,得到如下表格:
月份x | 1 | 2 | 3 | 4 | 5 |
体重超重的人数y | 640 | 540 | 420 | 300 | 200 |
若该大学体重超重人数y与月份变量x(月份变量x依次为1,2,3,4,5…)具有线性相关关系,请预测从第几月份开始该大学体重超重的人数降至10人以下?
(2)在某次排球训练课上,球恰由A队员控制,此后排球仅在A队员、B队员和C队员三人中传递,已知每当球由A队员控制时,传给B队员的概率为![]() ,传给C队员的概率为
,传给C队员的概率为![]() ;每当球由B队员控制时,传给A队员的概率为
;每当球由B队员控制时,传给A队员的概率为![]() ,传给C队员的概率为
,传给C队员的概率为![]() ;每当球由C队员控制时,传给A队员的概率为
;每当球由C队员控制时,传给A队员的概率为![]() ,传给B队员的概率为
,传给B队员的概率为![]() .记
.记![]() ,
,![]() ,
,![]() 为经过n次传球后球分别恰由A队员、B队员、C队员控制的概率.
为经过n次传球后球分别恰由A队员、B队员、C队员控制的概率.
(i)若![]() ,B队员控制球的次数为X,求
,B队员控制球的次数为X,求![]() ;
;
(ii)若![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,证明:
,证明:![]() 为等比数列,并判断经过200次传球后A队员控制球的概率与
为等比数列,并判断经过200次传球后A队员控制球的概率与![]() 的大小.
的大小.
附1:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: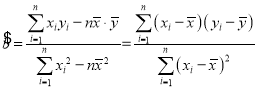 ;
;![]() .
.
附2:参考数据:![]() ,
,![]() .
.
【答案】(1)可以预测从第7月份开始该大学体重超重的人数降至10人以下;(2)(i)![]() (ii)证明见解析;
(ii)证明见解析;![]() .
.
【解析】
(1)利用回归直线方程计算公式,计算出回归直线方程,并由此进行预测.
(i)利用相互独立事件概率计算公式,计算出分布列,进而计算出![]() .
.
(ii)证明部分:法一:通过证明![]() 证得
证得![]() 为等比数列;法二:通过证明
为等比数列;法二:通过证明![]() 证得
证得![]() 为等比数列.
为等比数列.
求得数列![]() 的通项公式,由此判断出
的通项公式,由此判断出![]() .
.
(1)由已知可得:![]() ,
,
![]() ,
,
又因为![]() ,
,![]() ,
,
所以 ,
,
所以![]() ,
,
所以![]() ,
,
当![]() 时,
时,![]() ,
,
所以,可以预测从第7月份开始该大学体重超重的人数降至10人以下.
(2)(i)由题知X的可能取值为:0,1,2;
![]() ;
;
![]() ;
;
![]() ;
;
![]() 的分布列为:
的分布列为:
|
|
|
|
|
|
|
|
所以![]() .
.
(ii)(法一)由![]() ,
,![]() ,
,
两式相加得:![]() .
.
因为![]() ,
,
所以![]() ,
,![]() ,
,
代入等式得![]() ,即
,即![]()
所以![]() ,
,
因为![]() ,
,![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以数列![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,
的等比数列,
所以![]() ,
,
即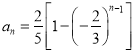 ,
,
因此经过200次传球后A队员控制球的概率
 .
.
(法二)由题知:![]() ,所以
,所以![]() ,
,
所以![]() ,
,
又因为![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以![]() ,
,
又因为![]() ,所以
,所以![]() ,
,
所以数列![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,
的等比数列,
所以![]() ,即
,即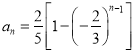 ,
,
因此经过200次传球后A队员控制球的概率 .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() 则x∈[﹣1,e]时,f(x)的最小值为_____;设g(x)=[f(x)]2﹣f(x)+a若函数g(x)有6个零点,则实数a的取值范围是_____.
则x∈[﹣1,e]时,f(x)的最小值为_____;设g(x)=[f(x)]2﹣f(x)+a若函数g(x)有6个零点,则实数a的取值范围是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,方程C:![]() 表示的曲线被称作“四叶玫瑰线”(如图)
表示的曲线被称作“四叶玫瑰线”(如图)

(1)求以极点为圆心的单位圆与四叶玫瑰线交点的极坐标和直角坐标;
(2)直角坐标系的原点与极点重合,x轴正半轴与极轴重合.求直线l:![]() 上的点M与四叶攻瑰线上的点N的距离的最小值.
上的点M与四叶攻瑰线上的点N的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年,某省将实施新高考,
年,某省将实施新高考,![]() 年秋季入学的高一学生是新高考首批考生,新高考不再分文理科,采用
年秋季入学的高一学生是新高考首批考生,新高考不再分文理科,采用![]() 模式,其中语文、数学、外语三科为必考科目,满分各
模式,其中语文、数学、外语三科为必考科目,满分各![]() 分,另外,考生还要依据想考取的高校及专业的要求,结合自己的兴趣爱好等因素,在思想政治、历史、地理、物理、化学、生物
分,另外,考生还要依据想考取的高校及专业的要求,结合自己的兴趣爱好等因素,在思想政治、历史、地理、物理、化学、生物![]() 门科目中自选
门科目中自选![]() 门参加考试(
门参加考试(![]() 选
选![]() ),每科目满分
),每科目满分![]() 分.为了应对新高考,某高中从高一年级
分.为了应对新高考,某高中从高一年级![]() 名学生(其中男生
名学生(其中男生![]() 人,女生
人,女生![]() 人)中,采用分层抽样的方法从中抽取n名学生进行调查.
人)中,采用分层抽样的方法从中抽取n名学生进行调查.
(1)已知抽取的n名学生中含女生![]() 人,求n的值及抽取到的男生人数;
人,求n的值及抽取到的男生人数;
(2)学校计划在高一上学期开设选修中的“物理”和“历史”两个科目,为了了解学生对这两个科目的选课情况,对在(1)的条件下抽取到的![]() 名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目),下面表格是根据调查结果得到的
名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目),下面表格是根据调查结果得到的![]() 列联表,请将下面的列联表补充完整,并判断是否有
列联表,请将下面的列联表补充完整,并判断是否有![]() 的把握认为选择科目与性别有关?说明你的理由;
的把握认为选择科目与性别有关?说明你的理由;
选择“物理” | 选择“历史” | 总计 | |
男生 | 10 | ||
女生 | 30 | ||
总计 |
(3)在抽取到的![]() 名女生中,在(2)的条件下,按选择的科目进行分层抽样,抽出
名女生中,在(2)的条件下,按选择的科目进行分层抽样,抽出![]() 名女生,了解女生对“历史”的选课意向情况,在这
名女生,了解女生对“历史”的选课意向情况,在这![]() 名女生中再抽取
名女生中再抽取![]() 人,求这
人,求这![]() 人中选择“历史”的人数为
人中选择“历史”的人数为![]() 人的概率.
人的概率.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为1,E,F分别是
的边长为1,E,F分别是![]() ,
,![]() 的中点,
的中点,![]() 交EF于点D,现沿SE,SF及EF把这个正方形折成一个四面体,使
交EF于点D,现沿SE,SF及EF把这个正方形折成一个四面体,使![]() ,
,![]() ,
,![]() 三点重合,重合后的点记为G,则在四面体
三点重合,重合后的点记为G,则在四面体![]() 中必有( )
中必有( )

A.![]() 平面EFG
平面EFG
B.设线段SF的中点为H,则![]() 平面SGE
平面SGE
C.四面体![]() 的体积为
的体积为![]()
D.四面体![]() 的外接球的表面积为
的外接球的表面积为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
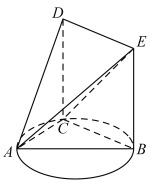
【题目】如图,点![]() 是以
是以![]() 为直径的圆上的动点(异于
为直径的圆上的动点(异于![]() ,
,![]() ),已知
),已知![]() ,
,![]() ,
,![]() 平面
平面![]() ,四边形
,四边形![]() 为平行四边形.
为平行四边形.
(1)求证:![]() 平面
平面![]() ;
;
(2)当三棱锥![]() 的体积最大时,求平面
的体积最大时,求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,焦距为
,焦距为![]() .
.
(1)求![]() 的方程;
的方程;
(2)若斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(点
两点(点![]() ,
,![]() 均在第一象限),
均在第一象限),![]() 为坐标原点.
为坐标原点.
①证明:直线![]() 的斜率依次成等比数列.
的斜率依次成等比数列.
②若![]() 与
与![]() 关于
关于![]() 轴对称,证明:
轴对称,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年7月1日迎来了我国建党98周年,6名老党员在这天相约来到革命圣地之一的西柏坡.6名老党员中有3名党员当年在同一个班,他们站成一排拍照留念时,要求同班的3名党员站在一起,且满足条件的每种排法都要拍一张照片,若将照片洗出来,每张照片0.5元(不含过塑费),且有一半的照片需要过塑,每张过塑费为0.75元.若将这些照片平均分给每名老党员(过塑的照片也要平均分),则每名老党员需要支付的照片费为( )
A.20.5B.21元C.21.5元D.22元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一场突如其来的新冠肺炎疫情在全国蔓延,在党中央的坚强领导和统一指挥下,全国人民众志成城、团结一心,共抗疫情。每天测量体温也就成为了所有人的一项责任,一般认为成年人腋下温度![]() (单位:℃)平均在36℃~37℃之间即为正常体温,超过37.1℃即为发热。发热状态下,不同体温可分成以下三种发热类型:低热:
(单位:℃)平均在36℃~37℃之间即为正常体温,超过37.1℃即为发热。发热状态下,不同体温可分成以下三种发热类型:低热:![]() ;高热:
;高热:![]() ;超高热(有生命危险):
;超高热(有生命危险):![]() .
.
某位患者因发热,虽排除肺炎,但也于12日至26日住院治疗. 医生根据病情变化,从14日开始,以3天为一个疗程,分别用三种不同的抗生素为该患者进行消炎退热. 住院期间,患者每天上午8:00服药,护士每天下午16:00为患者测量腋下体温记录如下:
抗生素使用情况 | 没有使用 | 使用“抗生素A”治疗 | 使用“抗生素B”治疗 | |||||
日期 | 12日 | 13日 | 14日 | 15日 | 16日 | 17日 | 18日 | 19日 |
体温(℃) | 38.7 | 39.4 | 39.7 | 40.1 | 39.9 | 39.2 | 38.9 | 39.0 |
抗生素使用情况 | 使用“抗生素C”治疗 | 没有使用 | |||||
日期 | 20日 | 21日 | 22日 | 23日 | 24日 | 25日 | 26日 |
体温(℃) | 38.4 | 38.0 | 37.6 | 37.1 | 36.8 | 36.6 | 36.3 |
(1)请你计算住院期间该患者体温不低于39℃的各天体温平均值;
(2)在18日—22日期间,医生会随机选取3天在测量体温的同时为该患者进行某一特殊项目“![]() 项目”的检查,求至少两天在高热体温下做“
项目”的检查,求至少两天在高热体温下做“![]() 项目”检查的概率;
项目”检查的概率;
(3)抗生素治疗一般在服药后2-8个小时就能出现血液浓度的高峰,开始杀灭细菌,达到消炎退热效果.假设三种抗生素治疗效果相互独立,请依据表中数据,判断哪种抗生素治疗效果最佳,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com