Question

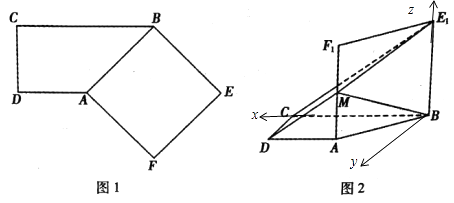
【题目】如图1，在直角梯形ABCD中，AD∥BC，AD⊥DC，BC=2AD=2DC，四边形ABEF是正方形．将正方形ABEF沿AB折起到四边形ABE1F1的位置，使平面ABE1F1⊥平面ABCD，M为AF1的中点，如图2．
（I）求证：AC⊥BM；
（Ⅱ）求平面CE1M与平面ABE1F1所成锐二面角的余弦值．

Answer 1

【答案】解：（Ⅰ）证明四边形ABE1F1是正方形，∴BE1⊥AB．

平面ABE1F1⊥平面ABCD，平面ABE1F1∩平面ABCD=AB，BE1面ABE1F1

∴BE1⊥平面ABCD，

∵AC平面ABCD，∴BE1⊥AC．

设AD=1，则AC=AB= ，∴AC⊥AB且AB∩BE1=B．

∴AC⊥面ABE1F1，又MB面ABE1F1∴AC⊥MB．

（Ⅱ）如图以B为原点，建立如图所示的空间直角坐标系．

则A（1，1，0），B（0，0，0），C（2，0，0），E1（0，0， ），M（1，1， ）．

由题意得， ， ， ，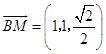

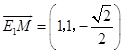设面CE1M的一个法向量为 ，

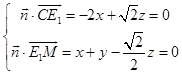，可得 ．

又平面ABE1F1得法向量为 ．

设平面CE1M与平面ABE1F1所成锐二面角为θ．

cosθ=|cos |= ．

∴平面CE1M与平面ABE1F1所成锐二面角的余弦值为 ．

【解析】（Ⅰ）只需证明BE1⊥AC．AC⊥AB且AB，可得AC⊥面ABE1F1，AC⊥MB．（Ⅱ）以B为原点，建立如图所示的空间直角坐标系．则A（1，1，0），B（0，0，0），C（2，0，0），E1（0，0， ），M（1，1， ）．利用向量求解
【考点精析】掌握直线与平面垂直的性质是解答本题的根本，需要知道垂直于同一个平面的两条直线平行．