
����Ŀ��2019����������������籭������2019���ڵı��������ݡ��Ͼ����Ϻ����人�����ڡ���ɽ����ݸ�������о���.Ϊ���������籭��ij��ѧ��ȫУѧ���������ȡ��![]() ��ѧ�������Ƿ��տ��������籭���µ�����������ʾ����飬ͳ���������£�
��ѧ�������Ƿ��տ��������籭���µ�����������ʾ����飬ͳ���������£�
���տ� | �����տ� | |
���� | 60 | 20 |
�� | 20 | 20 |
��1�������ϱ�˵�����ܷ���![]() �İ�����Ϊ�տ��������籭�������Ա��йأ�
�İ�����Ϊ�տ��������籭�������Ա��йأ�
��2���ִӲ����ʾ��������տ��������籭���µ�ѧ���У����ð��Ա�ֲ�����ķ���ѡȡ![]() �˲μ�2019����������������籭��־Ը�������.
�˲μ�2019����������������籭��־Ը�������.
��i�����С�Ůѧ����ѡȡ�����ˣ�
��ii��������![]() �������ѡȡ
�������ѡȡ![]() �˵�У�㲥վ��չ2019����������������籭���������ܣ���ǡ��ѡ��
�˵�У�㲥վ��չ2019����������������籭���������ܣ���ǡ��ѡ��![]() �������ĸ���.
�������ĸ���.
����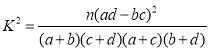 ������
������![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
���𰸡���1���У�2����i������![]() �ˣ�Ů��
�ˣ�Ů��![]() �ˣ�ii��
�ˣ�ii��![]()
��������
��1������ ����������ͨ���Ƚϼ����ж��ܷ���99%�İ�����Ϊ�տ���Ļʽ���Ա��йأ�
����������ͨ���Ƚϼ����ж��ܷ���99%�İ�����Ϊ�տ���Ļʽ���Ա��йأ�
��2�����������ݷֲ������������ý�ѡȡ��![]() ���У�������
���У�������![]() �ˣ�Ů����
�ˣ�Ů����![]() �ˣ�
�ˣ�
���������ȡ��![]() �������ֱ�Ϊ
�������ֱ�Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ��Ů��Ϊ�ף��г����г�ȡ���˵���������Լ��鵽
��Ů��Ϊ�ף��г����г�ȡ���˵���������Լ��鵽![]() �е������Ȼ�������ʣ�
�е������Ȼ�������ʣ�
������1����Ϊ![]()
![]() ��
��
������![]() �İ�����Ϊ�տ��������籭�����Ա��й�.
�İ�����Ϊ�տ��������籭�����Ա��й�.
��2����i�����ݷֲ���������ã�����![]() �ˣ�Ů��
�ˣ�Ů��![]() �ˣ�
�ˣ�
����ѡȡ��![]() ���У�������
���У�������![]() �ˣ�Ů����
�ˣ�Ů����![]() ��.
��.
��ii�����ȡ��![]() �������ֱ�Ϊ
�������ֱ�Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ��Ů��Ϊ�ף�
��Ů��Ϊ�ף�
���г�ȡ���ˣ��ֱ��Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ������
������
����![]() ���
���![]() ��
��![]() ��
��![]() ����
����![]() ������
������
���ԣ��������![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Ͷ�������εõ��ĵ����ֱ�Ϊm��n��������![]() ��m��n������
��m��n������![]() ��
��![]() ��1����1���ļнdz�Ϊֱ���������ڽǵĸ�����_____��
��1����1���ļнdz�Ϊֱ���������ڽǵĸ�����_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��![]() �������ڽ�
�������ڽ�![]() ��
��![]() ��
��![]() ����Ӧ�ı߷ֱ�Ϊ
����Ӧ�ı߷ֱ�Ϊ![]() ��
��![]() ��
��![]() ������
������![]() ��
��![]() ��������
��������![]() �������������
�������������![]() .
.
��1����֤��![]() ������߳�
������߳�![]() ��ֵ��
��ֵ��
��2���жϡ�![]() ����״������
����״������![]() ʱ����
ʱ����![]() �Ĵ�С.
�Ĵ�С.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�����C�IJ���������![]() ��
��![]() Ϊ��������������C�ĺ���������Ϊԭ����
Ϊ��������������C�ĺ���������Ϊԭ����![]() ������������Ϊԭ����һ�룬�õ�����
������������Ϊԭ����һ�룬�õ�����![]() ֱ��l����ͨ������
ֱ��l����ͨ������![]() ��������ԭ��OΪ���㣬x��������Ϊ���Ὠ��������ϵ.
��������ԭ��OΪ���㣬x��������Ϊ���Ὠ��������ϵ.
��1����ֱ��l�ļ����귽�̺�����![]() ����ͨ���̣�
����ͨ���̣�
��2��������![]() ��
��![]() ����
����![]() ���ڵ�A����l���ڵ�B����
���ڵ�A����l���ڵ�B����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �ĵ�����ֱ�����Σ�
�ĵ�����ֱ�����Σ� ![]() ��
�� ![]() ��
��
![]() ����
����![]() ���߶�
���߶�![]() �ϣ���
�ϣ���![]() ��
�� ![]() ��
�� ![]() ƽ��
ƽ��![]() .
.
��1����֤��ƽ��![]() ƽ��
ƽ��![]() ��
��
��2��������![]() ��������ʱ��������
��������ʱ��������![]() �ı����.
�ı����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������Ϸ�������أ���Ϸ�����ȴ���һ�أ�����һ�ش������ܽ���ڶ��أ����ض��������سɹ�����ÿ�ظ������δ��ػ���.��֪������һ��ÿ�δ����ĸ��ʾ�Ϊ![]() ���ڶ���ÿ�δ����ĸ��ʾ�Ϊ
���ڶ���ÿ�δ����ĸ��ʾ�Ϊ![]() .������������ÿ�δ��ػ��ᣬ��ÿ�δ��ػ���Ӱ��.
.������������ÿ�δ��ػ��ᣬ��ÿ�δ��ػ���Ӱ��.
(1)���ǡ�ô���3�βŴ��سɹ��ĸ��ʣ�
(2)�Ǽ״��صĴ���Ϊ![]() �����������
�����������![]() �ķֲ��к�����.��
�ķֲ��к�����.��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��������
��������![]() �϶��ж��壬���������
�϶��ж��壬���������![]() ����
����![]() ʱ��
ʱ��![]() ��
��![]() ���������
���������![]() ������
������![]() ��
��![]() �����ƺ���.
�����ƺ���.
��1����![]() ��
��![]() �ϵ����ƺ���
�ϵ����ƺ���![]() �Ľ���ʽ��
�Ľ���ʽ��
��2��֤�������![]() ������
������![]() �Ϻ�Ϊ��ֵ����
�Ϻ�Ϊ��ֵ����![]() ��
��![]() ������������[ע�����
������������[ע�����![]() ������
������![]() �Ϻ�Ϊ��ֵ����
�Ϻ�Ϊ��ֵ����![]() ������
������![]() ���Ǽ��������˽�������֤��������ֱ��Ӧ��]
���Ǽ��������˽�������֤��������ֱ��Ӧ��]
��3�����ã�2���Ľ��ۣ�����![]() ��
��![]() �ϵĵ�������.
�ϵĵ�������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ��
��![]() ����
����![]() ��ֱ��
��ֱ��![]() �ϵ�����һ�㣬��
�ϵ�����һ�㣬��![]() ��
��![]() �����ߣ��е�ֱ�Ϊ
�����ߣ��е�ֱ�Ϊ![]() ��
��![]() ����
����![]() Ϊ����ԭ��.
Ϊ����ԭ��.
��1����![]() ����
����![]() �������
�������
��2����![]() ��
��![]() ��
��![]() ������������Ϊ
������������Ϊ![]() ��
��![]() ��
��![]() ����֤��
����֤��![]() ��
��
��3�����![]() ����
����![]() ���Ƿ���������ĵ�
���Ƿ���������ĵ�![]() ��ʹ��
��ʹ��![]() ����ֱ��
����ֱ��![]() �ĶԳƵ�
�ĶԳƵ�![]() ��
��![]() �ϣ������ڣ����
�ϣ������ڣ����![]() �����꣬�������ڣ���˵������.
�����꣬�������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �����������ȵ�����
�����������ȵ�����![]() ����
����![]()
![]() ����
����![]() �����������������⣺
�����������������⣺
(1)���ڲ�����3�������![]() ��ʹ��
��ʹ��![]() ��
��
(2)������![]() ��ͨ�ʽΪ
��ͨ�ʽΪ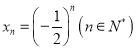 ����
����![]() ��
��![]() �������
�������
(3)������![]() �ǵȲ����У���
�ǵȲ����У���![]() ��
��![]() �������
�������
���������������ǣ� ��
A.(1)(2)B.(1)(3)C.(2)(3)D.(1)(2)(3)
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com