
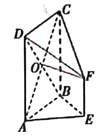
【题目】如图,在五面体![]() 中,侧面
中,侧面![]() 是正方形,
是正方形,![]() 是等腰直角三角形,点
是等腰直角三角形,点![]() 是正方形
是正方形![]() 对角线的交点
对角线的交点![]() ,
,![]() 且
且![]() .
.
(1)证明:![]() 平面
平面![]() ;
;
(2)若侧面![]() 与底面
与底面![]() 垂直,求五面体
垂直,求五面体![]() 的体积.
的体积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,证明四边形
,证明四边形![]() 为平行四边形,可得出
为平行四边形,可得出![]() ,再利用直线与平面平行的判定定理可证明出
,再利用直线与平面平行的判定定理可证明出![]() 平面
平面![]() ;
;
(2)取![]() 的中点
的中点![]() ,
,![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,将五面体
,将五面体![]() 分割为三棱柱
分割为三棱柱![]() 和四棱锥
和四棱锥![]() ,证明出
,证明出![]() 底面
底面![]() 和
和![]() 平面
平面![]() ,然后利用柱体和锥体体积公式计算出两个简单几何体的体积,相加可得出五面体
,然后利用柱体和锥体体积公式计算出两个简单几何体的体积,相加可得出五面体![]() 的体积.
的体积.
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,
,
![]() 侧面
侧面![]() 为正方形,且
为正方形,且![]() ,
,![]() 为
为![]() 的中点,
的中点,
又![]() 为
为![]() 的中点,
的中点,![]() 且
且![]() ,
,
![]() 且
且![]() ,
,![]() ,所以,四边形
,所以,四边形![]() 为平行四边形,
为平行四边形,![]() .
.
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ;
;
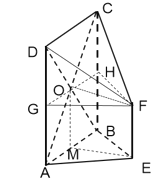
(2)取![]() 的中点
的中点![]() ,
,![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,
,
![]() 四边形
四边形![]() 为正方形,
为正方形,![]() .
.
![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 底面
底面![]() ,
,
易知![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() 为
为![]() 中点,
中点,![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
![]() ,
,![]() 、
、![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
![]() ,
,![]() 平面
平面![]() ,且
,且![]() ,
,
![]() ,因此,
,因此,![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象上所有点的横坐标缩短到原来的
的图象上所有点的横坐标缩短到原来的![]() 倍(纵坐标不变),再将所得的图象向左平移
倍(纵坐标不变),再将所得的图象向左平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图象.
的图象.
(1)写出函数![]() 的解析式;
的解析式;
(2)若对任意![]()
![]()
![]() ,
, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)求实数![]() 和正整数
和正整数![]() ,使得
,使得![]() 在
在![]() 上恰有
上恰有![]() 个零点.
个零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在△![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() 为
为![]() 的中点,
的中点, ![]() ,
,![]() .将△
.将△![]() 沿
沿![]() 折起到△
折起到△![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() ,
, ![]() 为
为![]() 的中点,如图2.
的中点,如图2.
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求F到平面A1OB的距离.

图1 图2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个结论中,错误的序号是___________.①以直角坐标系中![]() 轴的正半轴为极轴的极坐标系中,曲线C的方程为
轴的正半轴为极轴的极坐标系中,曲线C的方程为![]() ,若曲线C上总存在两个点到原点的距离为
,若曲线C上总存在两个点到原点的距离为![]() ,则实数
,则实数![]() 的取值范围是
的取值范围是![]() ;②在残差图中,残差点比较均匀地落在水平带状区域中,说明选用的模型比较合适,这样的带状区域宽度越宽,说明模型拟合精度越高;③设随机变量
;②在残差图中,残差点比较均匀地落在水平带状区域中,说明选用的模型比较合适,这样的带状区域宽度越宽,说明模型拟合精度越高;③设随机变量![]() ,若
,若![]() ,则
,则![]() ;④已知
;④已知![]() 为满足
为满足![]() 能被9整除的正数
能被9整除的正数![]() 的最小值,则
的最小值,则![]() 的展开式中,系数最大的项为第6项.
的展开式中,系数最大的项为第6项.
查看答案和解析>>
科目:高中数学 来源: 题型:
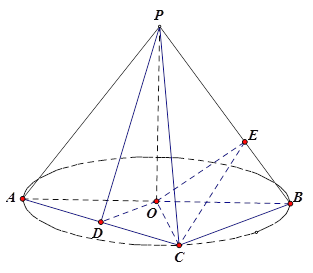
【题目】(本题满分12分)如图, ![]() 是圆
是圆![]() 的直径,点
的直径,点![]() 是圆
是圆![]() 上异于
上异于![]() 的点,
的点, ![]() 垂直于圆
垂直于圆![]() 所在的平面,且
所在的平面,且![]() .
.
(Ⅰ)若![]() 为线段
为线段![]() 的中点,求证
的中点,求证![]() 平面
平面![]() ;
;
(Ⅱ)求三棱锥![]() 体积的最大值;
体积的最大值;
(Ⅲ)若![]() ,点
,点![]() 在线段
在线段![]() 上,求
上,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人玩猜数字游戏,先由甲心中任想一个数字,记为![]() ,再由乙猜甲刚才想的数字把乙猜的数字记为
,再由乙猜甲刚才想的数字把乙猜的数字记为![]() ,且
,且![]() ,若
,若![]() ,则称甲乙“心有灵犀”,现任意找两个人玩这个游戏,得出他们“心有灵犀”的概率为________
,则称甲乙“心有灵犀”,现任意找两个人玩这个游戏,得出他们“心有灵犀”的概率为________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD为菱形,E为DD1中点.
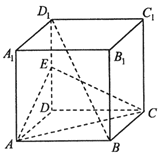
(1)求证:BD1∥平面ACE;
(2)求证:BD1⊥AC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF||AB,AB=2,BC=EF=1,AE=![]() ,DE=3,∠BAD=60,G为BC的中点.
,DE=3,∠BAD=60,G为BC的中点.
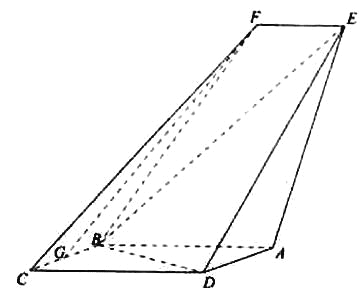
(Ⅰ)求证:FG||平面BED;
(Ⅱ)求证:平面BED⊥平面AED;
(Ⅲ)求直线EF与平面BED所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,AB=PA=1,AD![]() ,F是PB中点,E为BC上一点.
,F是PB中点,E为BC上一点.
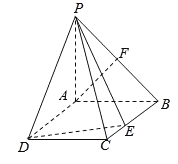
(1)求证:AF⊥平面PBC;
(2)当BE为何值时,二面角C﹣PE﹣D为45°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com