
【题目】已知函数f(x)=|x﹣a|,若不等式f(x)≤3的解集为{|x|﹣1≤x≤5}. (Ⅰ)求实数a的值:
(Ⅱ)若不等式f(3x)+f(x+3)≥m对一切实数x恒成立,求实数m的取值范围.
【答案】解:(Ⅰ)由f(x)≤3得|x﹣a|≤3.解得a﹣3≤x≤a+3.又不等式f(x)≤3的解集为{x|﹣1≤x≤5}. 所以 ![]() ,解得a=2.
,解得a=2.
(Ⅱ)由(Ⅰ)知f(x)=|x﹣2|,设函数g(x)=f(3x)+f(x+3),则 
所以函数g(x)的最小值为 ![]() .
.
由不等式f(3x)+f(x+3)≥m对一切实数x恒成立,得 ![]() .
.
于是实数m的取值范围为 ![]()
【解析】(1)由f(x)≤3得|x﹣a|≤3.得a﹣3≤x≤a+3.又不等式f(x)≤3的解集为{x|﹣1≤x≤5}.所以 ![]() ,解得a.(Ⅱ)由(Ⅰ)知f(x)=|x﹣2|,设函数g(x)=f(3x)+f(x+3),求出函数g(x)的最小值,m≤g(x)的最小值即可.
,解得a.(Ⅱ)由(Ⅰ)知f(x)=|x﹣2|,设函数g(x)=f(3x)+f(x+3),求出函数g(x)的最小值,m≤g(x)的最小值即可.
【考点精析】掌握绝对值不等式的解法是解答本题的根本,需要知道含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:高中数学 来源: 题型:
【题目】选修4﹣4;坐标系与参数方程 已知曲线C1的参数方程是 ![]() (φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立坐标系,曲线C2的坐标系方程是ρ=2,正方形ABCD的顶点都在C2上,且A,B,C,D依逆时针次序排列,点A的极坐标为(2,
(φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立坐标系,曲线C2的坐标系方程是ρ=2,正方形ABCD的顶点都在C2上,且A,B,C,D依逆时针次序排列,点A的极坐标为(2, ![]() ).
).
(1)求点A,B,C,D的直角坐标;
(2)设P为C1上任意一点,求|PA|2+|PB|2+|PC|2+|PD|2的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin2wx﹣sin2(wx﹣ ![]() )(x∈R,w为常数且
)(x∈R,w为常数且 ![]() <w<1),函数f(x)的图象关于直线x=π对称.
<w<1),函数f(x)的图象关于直线x=π对称.
(I)求函数f(x)的最小正周期;
(Ⅱ)在△ABC中,角A,B,C的对边分别为a,b,c,若a=1,f( ![]() A)=
A)= ![]() .求△ABC面积的最大值.
.求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为创建全国文明城市,某区向各事业行政单位征集“文明过马路”义务督导员.从符合条件的600名志愿者中随机抽取100名,按年龄作分组如下:[20,25),[25,30),[30,35),[35,40),[40,45],并得到如下频率分布直方图.
(Ⅰ)求图中x的值,并根据频率分布直方图统计这600名志愿者中年龄在[30.40)的人数;
(Ⅱ)在抽取的100名志愿者中按年龄分层抽取10名参加区电视台“文明伴你行”节目录制,再从这10名志愿者中随机选取3名到现场分享劝导制止行人闯红灯的经历,记这3名志愿者中年龄不低于35岁的人数为X,求X的分布列及数学期望.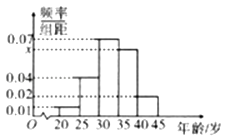
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市随机抽取部分企业调查年上缴税收情况(单位:万元),将所得数据绘制成频率分布直方图(如图),年上缴税收范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100]. (I)求直方图中x的值;
(Ⅱ)如果年上缴税收不少于60万元的企业可申请政策优惠,若共抽取企业1200个,试估计有多少企业可以申请政策优惠;
(Ⅲ)从企业中任选4个,这4个企业年上缴税收少于20万元的个数记为X,求X的分布列和数学期望.(以直方图中的频率作为概率)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个顶点的坐标为A(0,1),B(1,0),C(0,﹣2),O为坐标原点,动点M满足| ![]() |=1,则|
|=1,则| ![]() +
+ ![]() +
+ ![]() |的最大值是( )
|的最大值是( )
A.![]()
B.![]()
C.![]() ﹣1
﹣1
D.![]() ﹣1
﹣1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(2cosx,sinx),
=(2cosx,sinx), ![]() =(cosx,2
=(cosx,2 ![]() cosx),函数f(x)=
cosx),函数f(x)= ![]()
![]() ﹣1.
﹣1.
(Ⅰ)求函数f(x)的单调递减区间;
(Ⅱ)在锐角△ABC中,内角A、B、C的对边分别为a,b,c,tanB= ![]() ,对任意满足条件的A,求f(A)的取值范围.
,对任意满足条件的A,求f(A)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=2|x|﹣4的图象与曲线C:x2+λy2=4恰有两个不同的公共点,则实数λ的取值范围是( )
A.[﹣ ![]() ,
, ![]() )
)
B.[﹣ ![]() ,
, ![]() ]
]
C.(﹣∞,﹣ ![]() ]∪(0,
]∪(0, ![]() )
)
D.(﹣∞,﹣ ![]() ]∪[
]∪[ ![]() ,+∞)
,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com