
 22、如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B,C两点,圆心O在∠PAC的内部,点M是BC的中点.
22、如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B,C两点,圆心O在∠PAC的内部,点M是BC的中点.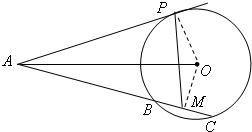 证明:(Ⅰ)连接OP,OM.
证明:(Ⅰ)连接OP,OM.

科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源:2010年海南省高二下学期期末测试数学文 题型:解答题
(本小题10分)
如图,已知AP是 O的切线,P为切点,AC是
O的切线,P为切点,AC是 O的割线,与
O的割线,与 O交于B,C两点,圆心O在
O交于B,C两点,圆心O在 PAC的内部,点M是BC的中点。
PAC的内部,点M是BC的中点。

(1) 证明:A,P,O,M四点共圆;
(2)
求 OAM+
OAM+ APM的大小。
APM的大小。
查看答案和解析>>
科目:高中数学 来源:2007年普通高等学校招生全国统一考试理科数学卷(海南) 题型:解答题
(本小题满分10分)选修4-1:几何证明选讲
 如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B、C两点,圆心O在
如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B、C两点,圆心O在 的内部,点M是BC的中点.
的内部,点M是BC的中点.
(Ⅰ)证明A,P,O,M四点共圆;
(Ⅱ)求∠OAM+∠APM的大小.
查看答案和解析>>
科目:高中数学 来源:2012年内蒙古赤峰市元宝山二中高考数学三模试卷(理科)(解析版) 题型:解答题
 如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B,C两点,圆心O在∠PAC的内部,点M是BC的中点.
如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B,C两点,圆心O在∠PAC的内部,点M是BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com