
【题目】设z1 , z2是复数,则下列命题中的假命题是( )
A.若|z1﹣z2|=0,则 ![]() =
= ![]()
B.若z1= ![]() ,则
,则 ![]() =z2
=z2
C.若|z1|=|z2|,则z1 ![]() =z2
=z2 ![]()
D.若|z1|=|z2|,则z12=z22
【答案】D
【解析】解:对(A),若|z1﹣z2|=0,则z1﹣z2=0,z1=z2,所以 ![]() 为真;
为真;
对(B)若 ![]() ,则z1和z2互为共轭复数,所以
,则z1和z2互为共轭复数,所以 ![]() 为真;
为真;
对(C)设z1=a1+b1i,z2=a2+b2i,若|z1|=|z2|,则 ![]() ,
,
![]() ,所以
,所以 ![]() 为真;
为真;
对(D)若z1=1,z2=i,则|z1|=|z2|为真,而 ![]() ,所以
,所以 ![]() 为假.
为假.
所以答案是:D.
【考点精析】掌握命题的真假判断与应用和复数的模(绝对值)是解答本题的根本,需要知道两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系;复平面内复数所对应的点到原点的距离,是非负数,因而两复数的模可以比较大小;复数模的性质:(1)![]() (2)
(2)![]() (3)若
(3)若![]() 为虚数,则
为虚数,则![]() .
.


科目:高中数学 来源: 题型:
【题目】在△ABC中,边a、b、c分别是角A、B、C的对边,且满足bcosC=(3a-c)cosB
(1)求cosB
(2)若△ABC的面积为4![]() ,b=4
,b=4![]() ,求△ABC的周长
,求△ABC的周长
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+2a|+|x﹣1|,a∈R.
(1)当a=1时,解不等式f(x)≤5;
(2)若f(x)≥2对于x∈R恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,“共享单车”的出现为市民“绿色出行”提供了极大的方便,某共享单车公司“Mobike”计划在甲、乙两座城市共投资120万元,根据行业规定,每个城市至少要投资40万元,由前期市场调研可知:甲城市收益![]() 与投入
与投入![]() (单位:万元)满足
(单位:万元)满足![]() ,乙城市收益
,乙城市收益![]() 与投入
与投入![]() (单位:万元)满足
(单位:万元)满足![]() ,设甲城市的投入为
,设甲城市的投入为![]() (单位:万元),两个城市的总收益为
(单位:万元),两个城市的总收益为![]() (单位:万元).
(单位:万元).
(1)当甲城市投资50万元时,求此时公司总收益;
(2)试问如何安排甲、乙两个城市的投资,才能使总收益最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]()
(1)判断并证明函数![]() 的奇偶性;
的奇偶性;
(2)判断并证明函数![]() 在
在![]() 上的单调性;
上的单调性;
(3)是否存在这样的负实数![]() ,使
,使![]() 对一切
对一切![]() 恒成立,若存在,试求出
恒成立,若存在,试求出![]() 取值的集合;若不存在,说明理由
取值的集合;若不存在,说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是由正整数构成的数表,用![]() 表示第
表示第![]() 行第
行第![]() 个数(
个数(![]() ). 此表中
). 此表中![]() ,每行中除首尾两数外,其他各数分别等于其“肩膀”上的两数之和.
,每行中除首尾两数外,其他各数分别等于其“肩膀”上的两数之和.

(1)写出数表的第6行(从左至右依次列出);
(2)设第![]() 行的第二个数为
行的第二个数为![]() ,求
,求![]() ;
;
(3)令![]() ,记
,记![]() 为数列
为数列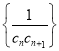 前
前![]() 项和,求
项和,求![]() 的最大值,并求此时
的最大值,并求此时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足:2a1+22a2+23a3+…+2nan=n(n∈N*),数列{ ![]() }的前n项和为Sn , 则S1S2S3…S10= .
}的前n项和为Sn , 则S1S2S3…S10= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据平面向量基本定理,若![]() 为一组基底,同一平面的向量
为一组基底,同一平面的向量![]() 可以被唯一确定地表示为
可以被唯一确定地表示为 ![]() =
= ![]() ,则向量
,则向量![]() 与有序实数对
与有序实数对![]() 一一对应,称
一一对应,称![]() 为向量
为向量![]() 的基底
的基底![]() 下的坐标;特别地,若
下的坐标;特别地,若![]() 分别为
分别为![]() 轴正方向的单位向量
轴正方向的单位向量![]() ,则称
,则称![]() 为向量
为向量![]() 的直角坐标.
的直角坐标.
(I)据此证明向量加法的直角坐标公式:若![]() ,则
,则![]() ;
;
(II)如图,直角![]() 中,
中, ![]() ,
, ![]() 点在
点在![]() 上,且
上,且![]() ,求向量
,求向量![]() 在基底
在基底![]() 下的坐标.
下的坐标.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 数列
数列![]() 的前
的前![]() 项和,对任意
项和,对任意![]() ,都有
,都有![]() (
(![]() 为常数).
为常数).
(1)当![]() 时,求
时,求![]() ;
;
(2)当![]() 时,
时,
(ⅰ)求证:数列![]() 是等差数列;
是等差数列;
(ⅱ)若对任意![]() ,必存在
,必存在![]() 使得
使得![]() ,已知
,已知![]() ,且
,且![]() ,
,
求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com