
【题目】根据平面向量基本定理,若![]() 为一组基底,同一平面的向量
为一组基底,同一平面的向量![]() 可以被唯一确定地表示为
可以被唯一确定地表示为 ![]() =
= ![]() ,则向量
,则向量![]() 与有序实数对
与有序实数对![]() 一一对应,称
一一对应,称![]() 为向量
为向量![]() 的基底
的基底![]() 下的坐标;特别地,若
下的坐标;特别地,若![]() 分别为
分别为![]() 轴正方向的单位向量
轴正方向的单位向量![]() ,则称
,则称![]() 为向量
为向量![]() 的直角坐标.
的直角坐标.
(I)据此证明向量加法的直角坐标公式:若![]() ,则
,则![]() ;
;
(II)如图,直角![]() 中,
中, ![]() ,
, ![]() 点在
点在![]() 上,且
上,且![]() ,求向量
,求向量![]() 在基底
在基底![]() 下的坐标.
下的坐标.

【答案】(I)见解析.(II)![]() .
.
【解析】试题分析:( I)利用平面向量的坐标运算即可证明结论成立;
( II)根据几何性质得出![]() ,用
,用![]() 、
、![]() 表示
表示![]() 即可;根据几何性质得出
即可;根据几何性质得出![]() ,再用
,再用![]() 、
、![]() 表示
表示![]() 即可.
即可.
试题解析:
(I)证明:根据题意: ![]()
![]()
∴![]() ,(4分)∴
,(4分)∴![]() .
.
(II)解:法一(向量法):根据几何性质,易知![]() ,
,
从而![]() ,所以
,所以![]() ,
,
化简得: ![]() ,所以
,所以![]() 在基底
在基底![]() 下的坐标为
下的坐标为![]() .
.
法二(向量法):同上可得: ![]() ,所以
,所以![]() .
.
上法也可直接从![]() 开始∴
开始∴![]() .
.
法三(向量法):设![]() ,则
,则![]() 利用
利用![]() 共线可解得.
共线可解得.
法四(坐标法):以![]() 为坐标原点,
为坐标原点, ![]() 方向为
方向为![]() 轴正方向建立直角坐标系(以下坐标法建系同),则
轴正方向建立直角坐标系(以下坐标法建系同),则![]() ,由几何意义易得
,由几何意义易得![]() 的直角坐标为
的直角坐标为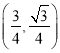 .
.
设![]() ,则
,则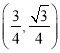 =
= ![]() ,又知
,又知![]() ,则由
,则由![]() 三点共线易得
三点共线易得![]() .
.
法六(坐标法):完全参照《必修4》P99例8(2)的模型和其解答过程,此处略.
法七(几何图形法):将![]() 分解在
分解在![]() 方向,利用平几知识算出边的关系亦可.
方向,利用平几知识算出边的关系亦可.
法八(向量法):设![]() ,则
,则![]() ①;
①;
由![]()
![]() ②,由①,②解得
②,由①,②解得![]() .
.
所以![]() 在基底
在基底![]() 下的坐标为
下的坐标为![]() .
.


科目:高中数学 来源: 题型:
【题目】空气质量问题,全民关注,有需求就有研究,某科研团队根据工地常用高压水枪除尘原理,制造了雾霾神器﹣﹣﹣雾炮,虽然雾炮不能彻底解决问题,但是能在一定程度上起到防霾、降尘的作用,经过测试得到雾炮降尘率的频率分布直方图:
若降尘率达到18%以上,则认定雾炮除尘有效.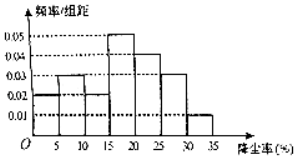
(1)根据以上数据估计雾炮除尘有效的概率;
(2)现把A市规划成三个区域,每个区域投放3台雾炮进行除尘(雾炮之间工作互不影响),若在一个区域内的3台雾炮降尘率都低于18%,则需对该区域后期追加投入20万元继续进行治理,求后期投入费用的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设z1 , z2是复数,则下列命题中的假命题是( )
A.若|z1﹣z2|=0,则 ![]() =
= ![]()
B.若z1= ![]() ,则
,则 ![]() =z2
=z2
C.若|z1|=|z2|,则z1 ![]() =z2
=z2 ![]()
D.若|z1|=|z2|,则z12=z22
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)左、右焦点分别为F1 , F2 , A(2,0)是椭圆的右顶点,过F2且垂直于x轴的直线交椭圆于P,Q两点,且|PQ|=3;
(a>b>0)左、右焦点分别为F1 , F2 , A(2,0)是椭圆的右顶点,过F2且垂直于x轴的直线交椭圆于P,Q两点,且|PQ|=3;
(1)求椭圆的方程;
(2)若直线l与椭圆交于两点M,N(M,N不同于点A),若 ![]()
![]() =0,
=0, ![]() =
= ![]() ;
;
①求证:直线l过定点;并求出定点坐标;
②求直线AT的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第35届牡丹花会期间,我班有5名学生参加志愿者服务,服务场所是王城公园和牡丹公园.
(1)若学生甲和乙必须在同一个公园,且甲和丙不能在同一个公园,则共有多少种不同的分配方案?
(2)每名学生都被随机分配到其中的一个公园,设X,Y分别表示5名学生分配到王城公园和牡丹公园的人数,记ξ=|X﹣Y|,求随机变量ξ的分布列和数学期望E(ξ)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】计划在某水库建一座至多安装 ![]() 台发电机的水电站,过去
台发电机的水电站,过去 ![]() 年的水文资料显示,水库年入流量
年的水文资料显示,水库年入流量 ![]() (年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上,不足
(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上,不足 ![]() 的年份有
的年份有 ![]() 年,不低于
年,不低于 ![]() 且不超过
且不超过 ![]() 的年份有
的年份有 ![]() 年,超过
年,超过 ![]() 的年份有
的年份有 ![]() 年,将年入流量在以上三段的频率作为相应段的概率,假设各年的年入流量相互独立.
年,将年入流量在以上三段的频率作为相应段的概率,假设各年的年入流量相互独立.
(1)求未来 ![]() 年中,设
年中,设 ![]() 表示流量超过
表示流量超过 ![]() 的年数,求
的年数,求 ![]() 的分布列及期望;
的分布列及期望;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量 ![]() 限制,并有如下关系:
限制,并有如下关系:
年入流量 |
|
|
|
发电机最多可运行台数 | 1 |
|
|
若某台发电机运行,则该台年利润为 ![]() 万元,若某台发电机未运行,则该台年亏损
万元,若某台发电机未运行,则该台年亏损 ![]() 万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com