
【题目】设A,B分别是双曲线![]() 的左右顶点,设过
的左右顶点,设过![]() 的直线PA,PB与双曲线分别交于点M,N,直线MN交x轴于点Q,过Q的直线交双曲线的于S,T两点,且
的直线PA,PB与双曲线分别交于点M,N,直线MN交x轴于点Q,过Q的直线交双曲线的于S,T两点,且![]() ,则
,则![]() 的面积( )
的面积( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:
【题目】某种证件的获取规则是:参加科目A和科目B的考试,每个科目考试的成绩分为合格与不合格,每个科目最多只有2次考试机会,且参加科目A考试的成绩为合格后,才能参加科目B的考试;参加某科目考试的成绩为合格后,不再参加该科目的考试,参加两个科目考试的成绩均为合格才能获得该证件.现有一人想获取该证件,已知此人每次参加科目A考试的成绩为合格的概率是![]() ,每次参加科目B考试的成绩为合格的概率是
,每次参加科目B考试的成绩为合格的概率是![]() ,且各次考试的成绩为合格与不合格均互不影响.假设此人不放弃按规则所给的所有考试机会,记他参加考试的次数为X.
,且各次考试的成绩为合格与不合格均互不影响.假设此人不放弃按规则所给的所有考试机会,记他参加考试的次数为X.
(1)求X的所有可能取的值;
(2)求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知2017年![]() 市居民平均家庭净收入走势图(家庭净收入=家庭总收入一家庭总支出),如图所示,则下列说法错误的是( )
市居民平均家庭净收入走势图(家庭净收入=家庭总收入一家庭总支出),如图所示,则下列说法错误的是( )

A. 2017年2月份![]() 市居国民的平均家庭净收入最低
市居国民的平均家庭净收入最低
B. 2017年4,5,6月份![]() 市居民的平均家庭净收入比7、8、9月份的平均家庭净收入波动小
市居民的平均家庭净收入比7、8、9月份的平均家庭净收入波动小
C. 2017年有3个月![]() 市居民的平均家庭净收入低于4000元
市居民的平均家庭净收入低于4000元
D. 2017年9、10、11、12月份平均家庭净收入持续降低
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平行四边形![]() 中,
中,![]() ,
,![]() ,过
,过![]() 点作
点作![]() 的垂线,交
的垂线,交![]() 的延长线于点
的延长线于点![]() ,
,![]() .连结
.连结![]() ,交
,交![]() 于点
于点![]() ,如图1,将
,如图1,将![]() 沿
沿![]() 折起,使得点
折起,使得点![]() 到达点
到达点![]() 的位置,如图2.
的位置,如图2.
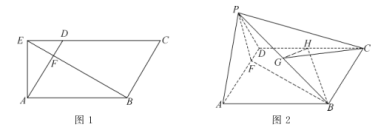
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,且平面
的中点,且平面![]() 平面
平面![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线![]() 的焦点为
的焦点为![]() ,过点
,过点![]() 作垂直于
作垂直于![]() 轴的直线与抛物线交于
轴的直线与抛物线交于![]() ,
,![]() 两点,且以线段
两点,且以线段![]() 为直径的圆过点
为直径的圆过点![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 为曲线
为曲线![]() :
:![]() 上的动点,求
上的动点,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,在圆
,在圆![]() :
:![]() 上任取一点
上任取一点![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() .(如图).
.(如图).

(1)求点![]() 的轨迹方程
的轨迹方程![]() ;
;
(2)若过点![]() 的动直线
的动直线![]() 与(1)中的轨迹
与(1)中的轨迹![]() 相交于
相交于![]() 、
、![]() 两点.问:平面内是否存在异于点
两点.问:平面内是否存在异于点![]() 的定点
的定点![]() ,使得
,使得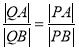 恒成立?试证明你的结论.
恒成立?试证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为方便市民出行,倡导低碳出行.某市公交公司推出利用支付宝和微信扫码支付乘车活动,活动设置了一段时间的推广期,在推广期内采用随机优惠鼓励市民扫码支付乘车.该公司某线路公交车队统计了活动推广期第一周内使用扫码支付的情况,其中![]() (单位:天)表示活动推出的天次,
(单位:天)表示活动推出的天次,![]() (单位:十人次)表示当天使用扫码支付的人次,整理后得到如图所示的统计表1和散点图.
(单位:十人次)表示当天使用扫码支付的人次,整理后得到如图所示的统计表1和散点图.
表1:
x | 第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | 第7天 |
y | 7 | 12 | 20 | 33 | 54 | 90 | 148 |

(1)由散点图分析后,可用![]() 作为该线路公交车在活动推广期使用扫码支付的人次
作为该线路公交车在活动推广期使用扫码支付的人次![]() 关于活动推出天次
关于活动推出天次![]() 的回归方程,根据表2的数据,求此回归方程,并预报第8天使用扫码支付的人次(精确到整数).
的回归方程,根据表2的数据,求此回归方程,并预报第8天使用扫码支付的人次(精确到整数).
表2:
|
|
| img src="http://thumb.zyjl.cn/questionBank/Upload/2019/08/08/08/88254471/SYS201908080801220877999013_ST/SYS201908080801220877999013_ST.008.png" width="67" height="40" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" /> |
|
|
4 | 52 | 3.5 | 140 | 2069 | 112 |
表中![]() ,
,![]() .
.
(2)推广期结束后,该车队对此期间乘客的支付情况进行统计,结果如表3.
表3:
支付方式 | 现金 | 乘车卡 | 扫码 |
频率 | 10% | 60% | 30% |
优惠方式 | 无优惠 | 按7折支付 | 随机优惠(见下面统计结果) |
统计结果显示,扫码支付中享受5折支付的频率为![]() ,享受7折支付的频率为
,享受7折支付的频率为![]() ,享受9折支付的频率为
,享受9折支付的频率为![]() .已知该线路公交车票价为1元,将上述频率作为相应事件发生的概率,记随机变量
.已知该线路公交车票价为1元,将上述频率作为相应事件发生的概率,记随机变量![]() 为在活动期间该线路公交车搭载乘客一次的收入(单位:元),求
为在活动期间该线路公交车搭载乘客一次的收入(单位:元),求![]() 的分布列和期望.
的分布列和期望.
参考公式:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为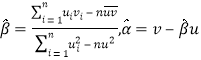 参考数据:
参考数据:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过抛物线x2=2py(p>0)的焦点,斜率为![]() 的直线交抛物线于A(x1,y1),B(x2,y2)(x1<x2)两点,且|AB|=9.
的直线交抛物线于A(x1,y1),B(x2,y2)(x1<x2)两点,且|AB|=9.
(1)求该抛物线的方程;
(2)O为坐标原点,C为抛物线上一点,若![]() ,求λ的值.
,求λ的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com