
【题目】已知函数f(x)=x2+4[sin(θ+![]() )]x﹣2,θ∈[0,2π].
)]x﹣2,θ∈[0,2π].
(Ⅰ)若函数f(x)为偶函数,求tanθ的值;
(Ⅱ)若f(x)在[﹣![]() ,1]上是单调函数,求θ的取值范围.
,1]上是单调函数,求θ的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ,或
,或![]() .
.
【解析】
试题分析:(Ⅰ)根据函数奇偶性的定义建立方程关系进行求解即可;(Ⅱ)利用一元二次函数的单调性的性质进行判断即可.
试题解析:(Ⅰ)∵f(x)是偶函数,∴f(﹣x)=f(x),
则x2+4[sin(θ+![]() )]x﹣2=x2﹣4[sin(θ+
)]x﹣2=x2﹣4[sin(θ+![]() )]x﹣2,
)]x﹣2,
则sin(θ+![]() )=0,
)=0,
∵θ∈[0,2π],∴θ+![]() =kπ,即θ=﹣
=kπ,即θ=﹣![]() +kπ,
+kπ,
∴tanθ=tan(﹣![]() +kπ)=﹣
+kπ)=﹣![]() .
.
(Ⅱ)∵f(x)=x2+4[sin(θ+![]() )]x﹣2,θ∈[0,2π]].
)]x﹣2,θ∈[0,2π]].
∴对称轴为x=﹣2sin(θ+![]() ),
),
若f(x)在[﹣![]() ,1]上是单调函数,
,1]上是单调函数,
则﹣2sin(θ+![]() )≥1或﹣2sin(θ+
)≥1或﹣2sin(θ+![]() )≤
)≤![]() ,
,
即sin(θ+![]() )≥
)≥![]() 或sin(θ+
或sin(θ+![]() )≤
)≤![]() ,
,
即2kπ+![]() ≤θ+
≤θ+![]() ≤2kπ+
≤2kπ+![]() ,或2kπ+
,或2kπ+![]() ≤θ+
≤θ+![]() ≤2kπ+
≤2kπ+![]() ,k∈Z,
,k∈Z,
即2kπ+![]() ≤θ≤2kπ+
≤θ≤2kπ+![]() ,或2kπ≤θ≤2kπ+
,或2kπ≤θ≤2kπ+![]() ,k∈Z,
,k∈Z,
∵θ∈[0,2π],∴![]() ≤θ≤
≤θ≤![]() ,或0≤θ≤
,或0≤θ≤![]() .
.


科目:高中数学 来源: 题型:
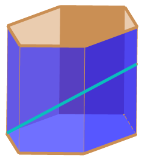
【题目】在我国瓷器的历史上六棱形的瓷器非常常见,因为六、八是中国人的吉利数字,所以好多瓷器都做成六棱形和八棱形.数学李老师有一个正六棱柱形状的笔筒,如图,底面边长为![]() ,高为
,高为![]() (底部及筒壁厚度忽略不计).一根长度为
(底部及筒壁厚度忽略不计).一根长度为![]() 的圆铁棒
的圆铁棒![]() (粗细忽略不计)斜放在笔筒内部,
(粗细忽略不计)斜放在笔筒内部,![]() 的一端置于正六棱柱某一侧棱的底端,另一端置于和该侧棱正对的侧棱上.一位小朋友玩耍时,向笔筒内注水,恰好将圆铁棒淹没,又将一个圆球放在笔筒口,球面又恰好接触水面,则球的表面积为______
的一端置于正六棱柱某一侧棱的底端,另一端置于和该侧棱正对的侧棱上.一位小朋友玩耍时,向笔筒内注水,恰好将圆铁棒淹没,又将一个圆球放在笔筒口,球面又恰好接触水面,则球的表面积为______![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数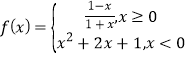 ,函数g(x)=f(1-x)-kx+k-
,函数g(x)=f(1-x)-kx+k-![]() 恰有三个不同的零点,则k的取值范围是( )
恰有三个不同的零点,则k的取值范围是( )
A. (-2-![]() ,0]∪
,0]∪![]() B. (-2+
B. (-2+![]() ,0]∪
,0]∪![]()
C. (-2-![]() ,0]∪
,0]∪![]() D. (-2+
D. (-2+![]() ,0]∪
,0]∪![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在
在![]() 上有两个零点,求实数m的取值范围;
上有两个零点,求实数m的取值范围;
(3)若对区间![]() 内任意两个不等的实数
内任意两个不等的实数![]() ,
,![]() ,不等式
,不等式![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
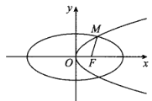
【题目】如图,已知椭圆![]() 的右焦点F为抛物线
的右焦点F为抛物线![]() 的焦点,点M为
的焦点,点M为![]() 和
和![]() 在第一象限的交点,且
在第一象限的交点,且![]() .
.
(Ⅰ)求抛物线![]() 的标准方程;
的标准方程;
(Ⅱ)若![]() ,过焦点F的直线l与
,过焦点F的直线l与![]() 相交于A,B两点,已知
相交于A,B两点,已知![]() ,求
,求![]() 取得最大值时直线l的方程.
取得最大值时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
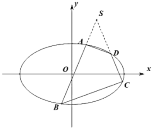
【题目】如图,在平面直角坐标系![]() 中,已知
中,已知![]() 分别是椭圆
分别是椭圆![]() :
:![]() (
(![]() )的左右焦点,点
)的左右焦点,点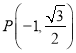 是椭圆
是椭圆![]() 上一点,且
上一点,且![]() .若椭圆
.若椭圆![]() 的内接四边形
的内接四边形![]() 的边
的边![]() 的延长线交于椭圆外一点
的延长线交于椭圆外一点![]() ,且点
,且点![]() 的横坐标为1,记直线
的横坐标为1,记直线![]() 的斜率分别为
的斜率分别为![]() ,
,![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com