
【题目】如图,已知椭圆![]() 的右焦点F为抛物线
的右焦点F为抛物线![]() 的焦点,点M为
的焦点,点M为![]() 和
和![]() 在第一象限的交点,且
在第一象限的交点,且![]() .
.
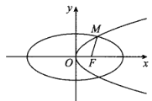
(Ⅰ)求抛物线![]() 的标准方程;
的标准方程;
(Ⅱ)若![]() ,过焦点F的直线l与
,过焦点F的直线l与![]() 相交于A,B两点,已知
相交于A,B两点,已知![]() ,求
,求![]() 取得最大值时直线l的方程.
取得最大值时直线l的方程.
【答案】(Ⅰ)![]() 或
或![]() ; (Ⅱ)
; (Ⅱ)![]() .
.
【解析】
(Ⅰ)设点![]() ,过M作
,过M作![]() 的准线的垂线,垂足为N,抛物线的准线与
的准线的垂线,垂足为N,抛物线的准线与![]() 轴的交点为
轴的交点为![]() ,根据焦半径公式可知
,根据焦半径公式可知![]() ,再根据椭圆定义可知
,再根据椭圆定义可知![]() ,结合直角
,结合直角![]() 和勾股定理,得
和勾股定理,得![]() ,所以点
,所以点![]() ,代入抛物线方程得
,代入抛物线方程得![]() ,建立方程求解
,建立方程求解![]() ;(Ⅱ)由(Ⅰ)和条件得到抛物线
;(Ⅱ)由(Ⅰ)和条件得到抛物线![]() ,设直线l的方程为
,设直线l的方程为![]() ,与抛物线方程联立,得到根与系数的关系
,与抛物线方程联立,得到根与系数的关系![]() ,
,![]() ,再代入
,再代入![]() 的坐标表示,得到
的坐标表示,得到![]() ,利用二次函数求最值,并得到直线方程.
,利用二次函数求最值,并得到直线方程.
(Ⅰ)设抛物线![]() 的标准方程为
的标准方程为![]() ,
,
椭圆![]() 的方程为
的方程为![]() ,半焦距为c.
,半焦距为c.
由已知得点![]() ,则
,则![]() .
.
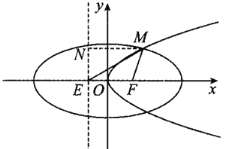
设点![]() ,过M作
,过M作![]() 的准线的垂线,垂足为N,抛物线的准线与
的准线的垂线,垂足为N,抛物线的准线与![]() 轴的交点为
轴的交点为![]() ,
,
由抛物线的定义,得![]() ,则
,则![]() .
.
根据椭圆定义,得![]() ,
,![]() ,
,
又因为![]() ,所以
,所以![]() .
.
所以点![]() ,代入抛物线方程得
,代入抛物线方程得![]() ,
,
从而![]() ,解得
,解得![]() 或
或![]() .
.
抛物线![]() 的标准方程为
的标准方程为![]() 或
或![]() .
.
(Ⅱ)抛物线![]() 和
和![]() 的焦点坐标分别为
的焦点坐标分别为![]() 和
和![]() 这时
这时![]() 或
或![]() ,
,
满足![]() 的只有抛物线
的只有抛物线![]() ,
,
设点![]() ,
,![]() ,
,
由题意知直线l的斜率不等于0,且过点![]() ,所以设直线l的方程为
,所以设直线l的方程为![]() ,
,
由 ,得
,得![]() ,
,
![]() 恒成立,
恒成立,
由韦达定理得![]() ,
,![]() ,
,
![]()
![]()
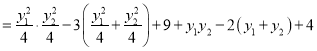
![]()
![]()
![]()
![]() ,
,
![]() 当
当![]() 时,
时,![]() 取最大值为
取最大值为![]() ,
,
此时直线l的方程为![]() .
.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:
【题目】足球运动是一项古老的体育活动,众多的资料表明,中国古代足球的出现比欧洲早,历史更为悠久,如图,现代比赛用足球是由正五边形与正六边形构成的共32个面的多面体,著名数学家欧拉证明了凸多面体的面数(F),顶点数(V),棱数(E)满足F+V-E=2,那么,足球有______.个正六边形的面,若正六边形的边长为![]() ,则足球的直径为______.cm(结果保留整数)(参考数据
,则足球的直径为______.cm(结果保留整数)(参考数据![]()

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+4[sin(θ+![]() )]x﹣2,θ∈[0,2π].
)]x﹣2,θ∈[0,2π].
(Ⅰ)若函数f(x)为偶函数,求tanθ的值;
(Ⅱ)若f(x)在[﹣![]() ,1]上是单调函数,求θ的取值范围.
,1]上是单调函数,求θ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 过点
过点![]() ,抛物线
,抛物线![]() 在
在![]() 处的切线交
处的切线交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作直线
作直线![]() 与抛物线
与抛物线![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,直线
,直线![]() 、
、![]() 、
、![]() 分别与抛物线的准线交于点
分别与抛物线的准线交于点![]() 、
、![]() 、
、![]() ,其中
,其中![]() 为坐标原点.
为坐标原点.
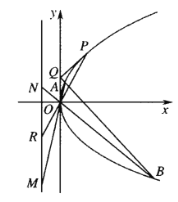
(Ⅰ)求抛物线![]() 的方程及其准线方程,并求出点
的方程及其准线方程,并求出点![]() 的坐标;
的坐标;
(Ⅱ)求证:![]() 为线段
为线段![]() 的中点.
的中点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 与过其右焦点F(1,0)的直线交于不同的两点A,B,线段AB的中点为D,且直线l与直线OD的斜率之积为
与过其右焦点F(1,0)的直线交于不同的两点A,B,线段AB的中点为D,且直线l与直线OD的斜率之积为![]() .
.
(1)求C的方程;
(2)设椭圆的左顶点为M,kMA,kMB分别表示直线MA,MB的斜率,求证![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD中,侧面PAD⊥底面ABCD,∠BAD=60°,△PAD是边长为2的正三角形,底面ABCD是菱形,点M为PC的中点.
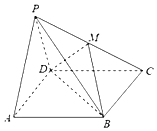
(1)求证:PA∥平面MDB;
(2)求三棱锥A﹣BDM的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年9月25日.阿里巴巴在杭州云栖大会上正式对外发布了含光800AI芯片,在业界标准的ResNet -50测试中,含光800推理性能达到78563lPS,比目前业界最好的AI芯片性能高4倍;能效比500 IPS/W,是第二名的3.3倍.在国内集成电路产业发展中,集成电路设计产业始终是国内集成电路产业中最具发展活力的领域,增长也最为迅速.如图是2014-2018年中国集成电路设计产业的销售额(亿元)及其增速(%)的统计图,则下面结论中正确的是( )
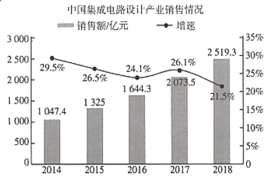
A.2014-2018年,中国集成电路设计产业的销售额逐年增加
B.2014-2017年,中国集成电路设计产业的销售额增速逐年下降
C.2018年中国集成电路设计产业的销售额的增长率比2015年的高
D.2018年与2014年相比,中国集成电路设计产业销售额的增长率约为110%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O为坐标原点,抛物线E的方程为x2=2py(p>0),其焦点为F,过点M (0,4)的直线![]() 与抛物线相交于P、Q两点且△OPQ为以O为直角顶点的直角三角形.
与抛物线相交于P、Q两点且△OPQ为以O为直角顶点的直角三角形.
(Ⅰ)求E的方程;
(Ⅱ)设点N为曲线E上的任意一点,证明:以FN为直径的圆与x轴相切.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com