分析:(1)由已知的双曲线方程及双曲线的性质可以求得A点坐标,由于已知过A作两条斜率分别为k1、k2的直线AM、AN交双曲线C于M、N两点,把直线MA的方程与双曲线的方程进行联立,利用韦达定理及xA=1,又k1k2=-m2可以M,N点的坐标的关系式,进而求解;
(2)由于∠MAN=60°,利用到角的定义可以知道AM到AN的角为60°或AN到AM的角为60°,进而得到两直线的斜率的关系等式,结合已知的两斜率的关系等式,联立解处斜率的数值,再利用直线的方程即可求得直线的方程.
解答:解:(1)C:
x2-=1的右顶点A坐标为(1,0)
设MA直线方程为y=k
1(x-1),代入m
2x
2-y
2-m
2=0中,整理得(m
2-k
1)x
2+2k
12x-(k
12+m
2)=0)
由韦达定理可知
xm•xA=,而x
A=1,又k
1k
2=-m
2∴
xm===于是
ym=k1(xm-1)=k1(-1)=由同理可知
yn=,于是有y
m=y
n∴MN∥x抽,从而MN直线率k
MN=0.
(2)∵∠MAN=60°,说明AM到AN的角为60°或AN到AM的角为60°.
则
=或
=,
又
k1k2=-(3+),k
1>k
2从而
则求得
或
因此MA,NA的直线的方程为y=x-1,
y=-(2+)(x-1)或为
y=(2+)(x-1),y=-(x-1).
点评:(1)此问考查了双曲线的右定点的定义,直线方程与双曲线方程联立后根与系数的关系,还考查了直线的斜率公式;
(2)此问考查了到角的定义及到角的公式,还考查了方程的思想,直线的点斜式求出直线的方程.



 的两个焦点为F1,F2,则这个椭圆上存在六个不同的点M,使得△F1MF2为直角三角形;
的两个焦点为F1,F2,则这个椭圆上存在六个不同的点M,使得△F1MF2为直角三角形; 的一个焦点作它的一条渐近线的垂线,垂足为M,O为坐标原点,则|OM|=a;
的一个焦点作它的一条渐近线的垂线,垂足为M,O为坐标原点,则|OM|=a;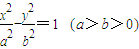 和圆O:x2+y2=b2(其中原点O为圆心),过双曲线C上一点P(x,y)引圆O的两条切线,切点分别为A、B.
和圆O:x2+y2=b2(其中原点O为圆心),过双曲线C上一点P(x,y)引圆O的两条切线,切点分别为A、B.