Question

在△PMN中，tan∠PMN= ,tan∠MNP=-2,且△PMN的面积为1，建立适当的坐标系，求以M、N为焦点，且过点P的椭圆的方程.

Answer 1

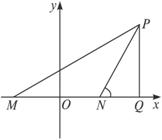
剖析：如下图，以直线MN为x轴，线段MN的垂直平分线为y轴，建立平面直角坐标系，则所求椭圆方程为+=1.显然a²、b²是未知数，但a²、b²与已知条件没有直接联系，因此应寻找与已知条件和谐统一的未知元，或改造已知条件.

解法一：如下图，过P作PQ⊥MN，垂足为Q，

    令|PQ|=m,于是可得

    |MQ|=|PQ|cot∠PMQ=2m,

    |QN|=|PQ|cot∠PNQ=m.

    ∴|MN|=|MQ|-|NQ|=2m-m=m.

    于是S_△PMN=|MN|·|PQ|=·m·m=1.

    因而m=,|MQ|=2,|NQ|=,|MN|=.

    |MP|=

    =

    =,

    |NP|=

    =

    =.

    以MN的中点为原点，MN所在直线为x轴建立直角坐标系，设椭圆方程为+=1(a＞b＞0).

    则2a=|MP|+|NP|=,

    2c=|MN|=,

    故所求椭圆方程为+=1.

解法二：设M(-c,0)、N(c,0),P(x,y),y＞0,

    则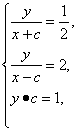

    解之，得x=,y=,c=.

    设椭圆方程为b²x²+a²y²=a²b²,则

   

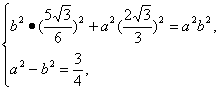
    解之，得a²=,b²=3.

    （以下略）

讲评：解法一选择了与a较接近的未知元|PM|、|PN|，但需改造已知条件，以便利用正弦定理和面积公式；解法二以条件为主，选择了与条件联系最直接的未知元x、y、c.本题解法较多，但最能体现方程思想方法的、学生易于理解和接受的是这两种解法.