
设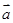 =(-1,1),
=(-1,1),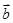 =(x,3),
=(x,3),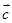 =(5,y),
=(5,y),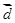 =(8,6),且
=(8,6),且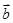 ∥
∥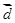 ,(4
,(4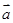 +
+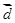 )⊥
)⊥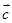 .
.
(1)求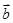 和
和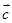 ;
;
(2)求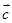 在
在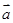 方向上的射影;
方向上的射影;
(3)求λ1和λ2,使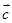 =λ1
=λ1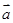 +λ2
+λ2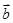 .
.
科目:高中数学 来源:江苏省扬州中学2011-2012学年高一下学期期中考试数学试题 题型:044
设等差数列{an}的前n项和为Sn,等比数列{bn}的前n项和为Tn,已知数列{bn}的公比为q(q>0),a1=b1=1,S5=45,T3=a3-b2.
(1)求数列{an},{bn}的通项公式;
(2)求![]()
查看答案和解析>>
科目:高中数学 来源:广州市2008届高中教材变式题1:集合与函数 题型:044
设函数y=f(x)定义在R上,对任意实数m、n,恒有f(m+n)=f(m)f(n)且当x>0,0<f(x)<1
(1)求证:f(0)=1,且当x<0时,f(x)>1;
(2)求证:f(x)在R上递减;
(3)设集合A={(x,y)|f(x2)·f(y2)>f(1)},B={(x,y)|f(ax-y+2)=1,a∈R},若A∩B=![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:广东省潮州金山中学2010-2011学年高二下学期期中考试数学文科试卷 题型:044
若实数m,n为关于x的一元二次方程Ax2+Bx+C=0的两个实数根,则有Ax2+Bx+C=A(x-m)(x-n),由系数可得:m+n=-![]() ,且m·n=
,且m·n=![]() .设x1,x2,x3为关于x的方程f(x)=x3-ax2+bx-c=0,(a,b,c∈R)的三个实数根.
.设x1,x2,x3为关于x的方程f(x)=x3-ax2+bx-c=0,(a,b,c∈R)的三个实数根.
(1)写出三次方程的根与系数的关系;即x1+x2+x3=_________;x1x2+x2x3+x3x1=_________;x1·x2·x3=_________
(2)若a,b,c均大于零,试证明:x1,x2,x3都大于零
(3)若a∈Z,b∈Z,|b|<2,f(x)在x=α,x=β处取得极值,且-1<α<β<1,求方程f(x)=0三个实根两两不相等时,实数c的取值范围.
查看答案和解析>>
科目:高中数学 来源:2008年高中数学集合与函数试题 题型:047
设函数y=f(x)定义在R上,对任意实数m、n,恒有f(m+n)=f(m)f(n)且当x>0,0<f(x)<1
(1)求证:f(0)=1,且当x<0时,f(x)>1;
(2)求证:f(x)在R上递减;
(3)设集合A={(x,y)|f(x2)·f(y2)>f(1)},B={(x,y)|f(ax-y+2)=1,a∈R},若A∩B=![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com