练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    (文)如图，在正方体ABCD－A1B1C1D1中，E、F、M分别是棱B1C1、B1B1、C1D1的中点.

    (Ⅰ)求证：CF⊥平面EAB；

    (Ⅱ)是否存在过E、M点且与平面A1FC平行的平面？若存在，请指出并证明之；若不存在，请说明理由.

    答案：
    解析：

    　　(Ⅰ)证明：在正方形B1BCC1中，∵E、F分别为B1C1、B1B的中点，

    　　∴△BB1E≌△BCF，∴∠B1BE＝∠BCF，

    　　∴∠BCF＋∠EBC＝90°，∴CF⊥BE

    　　又AB⊥平面B1BCC1，CF平面B1BCC1，

    　　∴AB⊥CF………………………………5分

    　　AB∩BE＝B，∴CF⊥平面EAB.…………6分

    　　(Ⅱ)设N是棱C1C上的一点，且C1N＝C1C.

    　　则平面EMN为符合要求的平面.…………8分

    　　证明如下：

    　　设H为棱C1C的中点，

    　　∵C1N＝C1C，

    　　∴C1N＝C1H，

    　　又E为B1C1的中点，

    　　∴EN//B1H，

    　　又CF//B1H，

    　　∴EN//CF，∴EN//平面A1FC………………………………10分

    　　同理MN//D1H，

    　　D1H//A1F，

    　　∴MN//A1F，∴MN//平面A1FC.………………………………11分

    　　EN∩MN＝N，

    　　∴平面EMN//平面A1FC.……………………………………12分


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

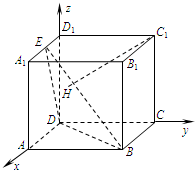    精英家教网[理]如图，在正方体ABCD-A1B1C1D1中，E是棱A1D1的中点，H为平面EDB内一点，
    HC1
    ={2m，-2m，-m}(m＜0)
    （1）证明HC1⊥平面EDB；
    （2）求BC1与平面EDB所成的角；
    （3）若正方体的棱长为a，求三棱锥A-EDB的体积．
    [文]若数列{an}的通项公式an=
    1
    (n+1)2
    (n∈N+)    ，记f（n）=（1-a1）（1-a2）…（1-an）．
    （1）计算f（1），f（2），f（3）的值；
    （2）由（1）推测f（n）的表达式；
    （3）证明（2）中你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （文）如图，在单位正方体ABCD-A1B1C1D1中，点P在线段AD1上运动，给出以下四个命题：
    ①异面直线A1P与BC1间的距离为定值；
    ②三棱锥D-BPC1的体积为定值；
    ③异面直线C1P与直线CB1所成的角为定值；
    ④二面角P-BC1-D的大小为定值．其中真命题有（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

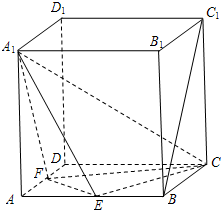    （2007•静安区一模）（文）如图，在棱长为2的正方体ABCD-A1B1C1D1中，点E、F分别是棱AB、AD的中点．求：
    （1）异面直线BC1与EF所成角的大小；
    （2）三棱锥A1-EFC的体积V．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （07年福建卷文）如图，在正方体ABCD-A1B1C1D1中，E、F、G、H分别为AA1、AB、BB1、BC1的中点，则异面直线EF与GH所成的角等于

    A.45°                                B.60°                     C.90°                    D.120°

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （08年中卫一中三模文）如图，在棱长为2的正方体中，、分别为、的中点．

    （1）求证：//平面；      

    （2）求证：；

     

    查看答案和解析>>

    同步练习册答案