
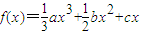 (a>0).
(a>0).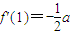 ,3a>2c>2b,证明:函数f(x)在区间(0,2)内一定有极值点;
,3a>2c>2b,证明:函数f(x)在区间(0,2)内一定有极值点;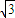 ,求
,求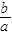 的取值范围.
的取值范围.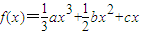 =0的三个实数根,则x3=0,结合韦达定理得出
=0的三个实数根,则x3=0,结合韦达定理得出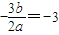 ,
,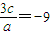 ,由此f′(x)=a(x-1)(x+3),单调区间可求.
,由此f′(x)=a(x-1)(x+3),单调区间可求.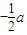 <0,整理3a+2b+2c=0,又f′(2)=4a+2b+c=4a-(3a+2c)+c=a-c.考察f′(0),f′(1),f′(2)的符号,利用f′(x)在(0,2)内由零点(需对c的取值进行讨论)进行证明.
<0,整理3a+2b+2c=0,又f′(2)=4a+2b+c=4a-(3a+2c)+c=a-c.考察f′(0),f′(1),f′(2)的符号,利用f′(x)在(0,2)内由零点(需对c的取值进行讨论)进行证明.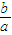 的不等式,并结合约束条件2c=-3a-2b,3a>2c>2b得出取值范围.
的不等式,并结合约束条件2c=-3a-2b,3a>2c>2b得出取值范围.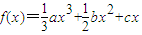 =x(
=x( )(a>0),又x1+x2+x3=-3,x1x2=-9,则x3=0,x1+x2=-3,x1x2=-9(1分)
)(a>0),又x1+x2+x3=-3,x1x2=-9,则x3=0,x1+x2=-3,x1x2=-9(1分)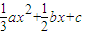 =0的两根,
=0的两根,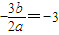 ,
,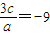 ,得
,得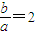 ,
,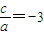 ,(3分)
,(3分) =a(x2+2x-3)=a(x-1)(x+3).
=a(x2+2x-3)=a(x-1)(x+3). ,,所以a+b+c=
,,所以a+b+c= ,即3a+2b+2c=0.
,即3a+2b+2c=0.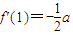 <0,f′(0)=c,f′(2)=4a+2b+c=4a-(3a+2c)+c=a-c.(8分)
<0,f′(0)=c,f′(2)=4a+2b+c=4a-(3a+2c)+c=a-c.(8分) <0,而f′(x)在区间(0,1)内连续,则f′(x)在区间(0,1)内至少有一个零点,设为x=m,则在x∈(0,m),f′(x)>0,
<0,而f′(x)在区间(0,1)内连续,则f′(x)在区间(0,1)内至少有一个零点,设为x=m,则在x∈(0,m),f′(x)>0,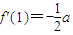 <0,f′(2)=a-c>0,则f′(x)在区间(1,2)内至少有一零点.
<0,f′(2)=a-c>0,则f′(x)在区间(1,2)内至少有一零点.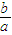 ,mn=
,mn=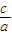 =
=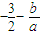 .所以|m-n|=
.所以|m-n|=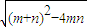 =
= =
=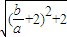
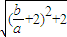
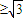 ,则两边平方
,则两边平方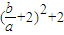 ≥3,得出
≥3,得出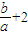 ≥1,或
≥1,或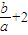 ≤-1,即
≤-1,即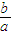 ≥-1,或
≥-1,或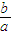 ≤-3
≤-3 a.
a.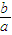 <-
<- .
.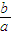 的取值范围是[-1,-
的取值范围是[-1,- ).
).

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源:2014届广东省高三第一次月考理科数学试卷(解析版) 题型:选择题
已知函数 ,
, (a>0),若
(a>0),若 ,
, ,使得f(x1)= g(x2),则实数a的取值范围是( )
,使得f(x1)= g(x2),则实数a的取值范围是( )
(A)  (B)
(B)
 (C)
(C)
 (D)
(D)

查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省淄博一中高一(上)期中数学试卷(解析版) 题型:解答题
 (a>0,且a≠1)
(a>0,且a≠1)查看答案和解析>>
科目:高中数学 来源:《三角函数》2013年广东省十二大市高三二模数学试卷汇编(理科)(解析版) 题型:选择题
 (A>0,ω>0,x∈(-∞,+∞))的最小正周期为π,且
(A>0,ω>0,x∈(-∞,+∞))的最小正周期为π,且 ,则函数y=f(x)在
,则函数y=f(x)在 上的最小值是( )
上的最小值是( )


查看答案和解析>>
科目:高中数学 来源:2010-2011学年四川省成都市高三上学期九月诊断性考试理科数学卷 题型:解答题
(本题满分12分)
已知函数 其中a>0,e为自然对数的底数。
其中a>0,e为自然对数的底数。
(I)求
(II)求 的单调区间;
的单调区间;
(III)求函数 在区间[0,1]上的最大值。
在区间[0,1]上的最大值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com