练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】对有个元素的总体进行抽样，先将总体分成两个子总体和（是给定的正整数，且），再从每个子总体中各随机抽取2个元素组成样本.用表示元素和同时出现在样本中的概率.

    （1）求的表达式（用，表示）；

    （2）求所有的和.

    【答案】（1） ；（2）6

    【解析】

    （1）根据组合数的公式，以及古典概型的概率计算公式和相互独立事件的概率计算公式，即可求解；

    （2）当都在中时求得的和为1，当同时在中时，求得的和为1，当在中，在中时得到的和为4，即可求解.

    （1）由题意，从和个式子中随机抽取2个，分别有和个基本事件，

    所以的表达式为.

    （2）当都在中时，可得，

    而从中选两个数的不同方法数为，则的和为1；

    当同时在中时，同理可得的和为1；

    当在中，在中时，，

    而从中选取一个数，从中选一个数的不同方法数为，

    则的和为4，所以所有的和为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】检验中心为筛查某种疾病，需要检验血液是否为阳性，对份血液样本，有以下两种检验方式：①逐份检验，需要检验次；②混合检验，即将其中（且）份血液样本分别取样混合在一起检验，若检验结果为阴性，这份的血液全为阴性，因而这份血液样本只要检验一次就够了，如果检验结果为阳性，为了明确这份血液究竟哪几份为阳性，再对这份再逐份检验，此时这份血液的检验次数总共为次.假设在接受检验的血液样本中，每份样本的检验结果是阳性还是阴性都是独立的，且每份样本是阳性结果的概率为.

    （1）假设有5份血液样本，其中只有2份样本为阳性，若采用逐份检验方式，求恰好经过2次检验就能把阳性样本全部检验出来的概率；

    （2）现取其中（且）份血液样本，记采用逐份检验方式，样本需要检验的总次数为，采用混合检验方式，样本需要检验的总次数为点.当时，根据和的期望值大小，讨论当取何值时，采用逐份检验方式好？

    （参考数据：，，，，，.）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】随着运动app和手环的普及和应用，在朋友圈、运动圈中出现了每天1万步的健身打卡现象，“日行一万步，健康一辈子”的观念广泛流传.“健步达人”小王某天统计了他朋友圈中所有好友（共500人）的走路步数，并整理成下表：

    分组（单位：千步）

    频数

    60

    240

    100

    60

    20

    18

    0

    2

    （1）请估算这一天小王朋友圈中好友走路步数的平均数（同一组中数据以这组数据所在区间中点值作代表）；

    （2）若用表示事件“走路步数低于平均步数”，试估计事件发生的概率；

    （3）若称每天走路不少于8千步的人为“健步达人”，小王朋友圈中岁数在40岁以上的中老年人共有300人，其中健步达人恰有150人，请填写下面列联表.根据列联表判断，有多大把握认为，健步达人与年龄有关？

    健步达人

    非健步达人

    合计

    40岁以上

    不超过40岁

    合计

    附：.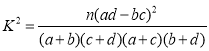

    0.050

    0.010

    0.001

    3.841

    6.635

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，为抛物线上不同的两点，且，点且于点.

    （1）求的值；

    （2）过轴上一点 的直线交于，两点，在的准线上的射影分别为，为的焦点，若，求中点的轨迹方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

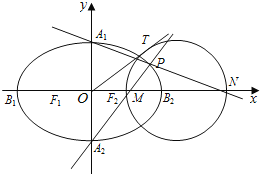
    【题目】已知椭圆的离心率，椭圆C的上、下顶点分别为A1，A2，左、右顶点分别为B1，B2，左、右焦点分别为F1，F2.原点到直线A2B2的距离为.

    （1）求椭圆C的方程；

    （2）P是椭圆上异于A1，A2的任一点，直线PA1，PA2，分别交x轴于点N，M，若直线OT与以MN为直径的圆G相切，切点为T.证明：线段OT的长为定值，并求出该定值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}满足a1＝1，an＝(n∈N*，n≥2)，数列{bn}满足关系式bn＝(n∈N*)．

    (1)求证：数列{bn}为等差数列；

    (2)求数列{an}的通项公式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数.

    （1）当时，求函数的零点个数；

    （2）若，使得，求实数m的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】直角坐标系xOy中，椭圆（a＞b＞0）的短轴长为，离心率为.

    （1）求椭圆的方程；

    （2）斜率为1且经过椭圆的右焦点的直线交椭圆于P1、P2两点，P是椭圆上任意一点，若（λ，μ∈R），证明：λ2+μ2为定值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

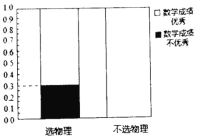
    【题目】某省即将实行新高考，不再实行文理分科.某校为了研究数学成绩优秀是否对选择物理有影响，对该校2018级的1000名学生进行调查，收集到相关数据如下：

    （1）根据以上提供的信息，完成列联表，并完善等高条形图；

    选物理

    不选物理

    总计

    数学成绩优秀

    数学成绩不优秀

    260

    总计

    600

    1000

    （2）能否在犯错误的概率不超过0.05的前提下认为数学成绩优秀与选物理有关？

    附：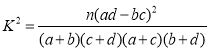

    临界值表：

    0.10

    0.05

    0.010

    0.005

    0.001

    2.706

    3.841

    6.635

    7.879

    10.828

    查看答案和解析>>

    同步练习册答案