
【题目】将函数y=sin(2x﹣ ![]() )的图象先向左平移
)的图象先向左平移 ![]() 个单位,再将图象上各点的横坐标变为原来的
个单位,再将图象上各点的横坐标变为原来的 ![]() 倍(纵坐标不变),那么所得图象的解析式为y= .
倍(纵坐标不变),那么所得图象的解析式为y= .
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:
【题目】某工厂生产甲、乙两种产品所得利润分别为P和Q(万元),它们与投入资金m(万元)的关系有经验公式P= ![]() m+65,Q=76+4
m+65,Q=76+4 ![]() ,今将150万元资金投入生产甲、乙两种产品,并要求对甲、乙两种产品的投资金额不低于25万元.
,今将150万元资金投入生产甲、乙两种产品,并要求对甲、乙两种产品的投资金额不低于25万元.
(1)设对乙产品投入资金x万元,求总利润y(万元)关于x的函数关系式及其定义域;
(2)如何分配使用资金,才能使所得总利润最大?最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx﹣ ![]() )(其中A,ω为常数,且A>0,ω>0)的部分图象如图所示.
)(其中A,ω为常数,且A>0,ω>0)的部分图象如图所示. 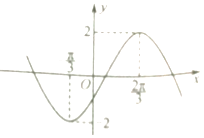
(1)求函数f(x)的解析式;
(2)若f(α+ ![]() )=
)= ![]() ,f(β+
,f(β+ ![]() )=
)= ![]() ,且α,β∈(0,
,且α,β∈(0, ![]() ),求α+β的值.
),求α+β的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在原点,焦点在x轴上,离心率等于 ![]() ,它的一个短轴端点是(0,2
,它的一个短轴端点是(0,2 ![]() ).
). 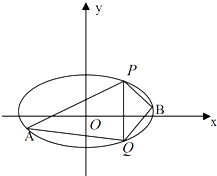
(1)求椭圆C的方程;
(2)P(2,3)、Q(2,﹣3)是椭圆上两点,A、B是椭圆位于直线PQ两侧的两动点,
①若直线AB的斜率为 ![]() ,求四边形APBQ面积的最大值;
,求四边形APBQ面积的最大值;
②当A、B运动时,满足∠APQ=∠BPQ,试问直线AB的斜率是否为定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆的中心在原点O,短轴长为 ![]() ,左焦点为F(﹣c,0)(c>0),直线
,左焦点为F(﹣c,0)(c>0),直线 ![]() 与x轴交于点A,且
与x轴交于点A,且 ![]() ,过点A的直线与椭圆相交于P,Q两点.
,过点A的直线与椭圆相交于P,Q两点. 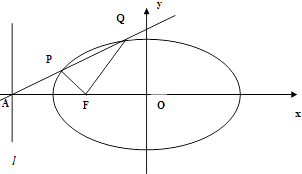
(1)求椭圆的方程.
(2)若 ![]() ,求直线PQ的方程.
,求直线PQ的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)定义域为[0,+∞),当x∈[0,1]时,f(x)=sinπx,当x∈[n,n+1]时,f(x)= ![]() ,其中n∈N,若函数f(x)的图象与直线y=b有且仅有2016个交点,则b的取值范围是( )
,其中n∈N,若函数f(x)的图象与直线y=b有且仅有2016个交点,则b的取值范围是( )
A.(0,1)
B.( ![]() ,
, ![]() )
)
C.( ![]() ,
, ![]() )
)
D.( ![]() ,
, ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com