练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知,函数其中

    （1）讨论函数的单调性；

    （2）若函数有两个零点，

    (i)求的取值范围；

    (ii)设的两个零点分别为x1,x2，证明：x1x2>e2．

    【答案】（1）见解析（2）(i)；(ii)见解析

    【解析】

    （1）求导后，分别在和两种情况下讨论导函数的符号，从而得到单调区间；（2）(i)将问题转化为与函数的图象在上有两个不同交点，通过求解相切时的临界值，得到的取值范围；(ii)将问题转化为证明成立，通过构造函数，证得，从而证得结论.

    （1）函数的定义域为，

    ①当时，，在单调递增；

    ②当时，由得，

    则当时，，在单调递增；

    当时，，在单调递减

    （2）(i)函数有两个零点即方程在有两个不同根

    转化为函数与函数的图象在上有两个不同交点

    如图：

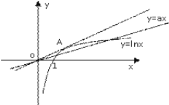
    可见，若令过原点且切于函数图象的直线斜率为，只需

    设切点，所以

    又，所以，解得

    于是，所以

    (ii)原不等式

    不妨设

    ，

    令，则，于是

    设函数，

    求导得：

    故函数是上的增函数

    即不等式成立，故所证不等式成立

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知，两点，满足:，，，则的最大值为________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

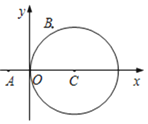
    【题目】如图，在平面直角坐标系xOy中，已知圆C：x2+y2-4x=0及点A（-1，0），B（1，2）

    （1）若直线l平行于AB，与圆C相交于M，N两点，MN=AB，求直线l的方程；

    （2）若圆C上存在两个点P，使得PA2+PB2=a（a＞4），求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，圆经过伸缩变换后得到曲线．以坐标原点为极点，轴的正半轴为极轴，并在两种坐标系中取相同的单位长度，建立极坐标系，直线的极坐标方程为．

    （1）求曲线的直角坐标方程及直线的直角坐标方程；

    （2）设点是上一动点，求点到直线的距离的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】判断下列命题的真假：

    （1）是的必要条件；

    （2）是的充要条件；

    （3）两个三角形的两组对应角相等是这两个三角形相似的充要条件；

    （4）三角形的三条边满足勾股定理是这个三角形为直角三角形的充要条件；

    （5）在中，重心和垂心重合是为等边三角形的必要条件；

    （6）如果点到点的距离相等，则点一定在线段的垂直平分线上.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知曲线.

    （1）当时，求曲线在处的切线方程；

    （2）过点作曲线的切线，若所有切线的斜率之和为1，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在数列中，，

    （I）求，，的值，由此猜想数列的通项公式：

    （Ⅱ）用数学归纳法证明你的猜想.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某同学用“五点法”画函数f(x)=Asin(ωx+)(A>0，ω>0，||<)在某一个周期内的图象时，列表并填入了部分数据，如表：

    ωx+

    0

    π

    2π

    x

    Asin(ωx+)

    0

    5

    -5

    0

    （1）请将上表数据补充完整，并求出函数f(x)的解析式；

    （2）将y=f(x)的图象向左平移个单位，得到函数y=g(x)的图象.若关于x的方程g(x)-m=0在区间[0，]上有两个不同的解，求实数m的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】剪纸艺术是最古老的中国民间艺术之一，作为一种镂空艺术，它能给人以视觉上以透空的感觉和艺术享受.在中国南北方的剪纸艺术，通过一把剪刀、一张纸、就可以表达生活中的各种喜怒哀乐.如图是一边长为1的正方形剪纸图案，中间黑色大圆与正方形的内切圆共圆心，圆与圆之间是相切的，且中间黑色大圆的半径是黑色小圆半径的2倍，若在正方形图案上随机取一点，则该点取自白色区域的概率为（ ）

    A.B.C.D.

    查看答案和解析>>

    同步练习册答案