
(Ⅰ)证明∠MDC是二面角M-AB-C的平面角;
(Ⅱ)当∠MDC =∠CVN时,证明VC⊥平面AMB;
(Ⅲ)若∠MDC =∠CVN =θ(![]() ),求四面体MABC的体积.
),求四面体MABC的体积.
| (Ⅰ)证明:
由已知, CD⊥AB,VN⊥平面ABC,N∈CD, ∴VN⊥AB. ∴AB⊥平面VNC. 又 V、M、N、D都在VNC所在的平面内, 所以,DM与VN必相交,且AB⊥DM,AB⊥CD, ∴∠MDC为二面角M-AB-C的平面角.
(Ⅱ)证明: 由已知,∠MDC =∠CVN, 在△VNC与△DMC中, ∠NCV =∠MCD, 又∵∠VNC =90º, ∴ ∠DMC =∠VNC =90º, 故有DM⊥VC,又AB⊥VC, ∴ VC⊥平面AMB. (Ⅲ)解: 由(Ⅰ)、(Ⅱ), MD⊥AB,MD⊥VC,且D∈AB,M∈VC, ∴ 又 ∵ ∠MDC =θ. 在Rt△MDC中, CM = V四面体MABC =V三棱锥C-ABM
|


科目:高中数学 来源: 题型:
 (2013•松江区二模)如图,已知ABC-A1B1C1是正三棱柱,它的底面边长和侧棱长都是2.
(2013•松江区二模)如图,已知ABC-A1B1C1是正三棱柱,它的底面边长和侧棱长都是2.查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 4 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:047
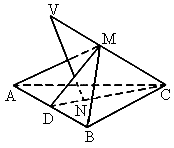
如图所示,已知V是△ABC所在平面外一点,VN垂直于平面ABC,且垂足N在△ABC的高CD上,M是VC上的一点,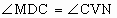 .
.
求证:VC⊥平面AMB.
查看答案和解析>>
科目:高中数学 来源:2008年上海市静安区高考数学二模试卷(文理合卷)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com