
(本小题满分12分)
数列 的前
的前 项和为
项和为 ,若
,若 ,点
,点 在直线
在直线 上.
上.
⑴求证:数列 是等差数列;
是等差数列;
⑵若数列 满足
满足 ,求数列
,求数列 的前
的前 项和
项和 ;
;
⑶设 ,求证:
,求证: .
.
(1)根据点 在直线
在直线
 上,那么得到
上,那么得到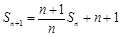 ,两边同时除以n得到结论。
,两边同时除以n得到结论。
(2) (3)根据
(3)根据 ,利用分组求和法来求解数列的和式,进而放缩得到结论。
,利用分组求和法来求解数列的和式,进而放缩得到结论。
解析试题分析:)⑴∵点 在直线
在直线
 上,
上,
∴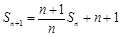 .
.
两边同除以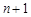 ,得
,得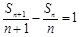 ,
,
于是 是以
是以 为首项,
为首项,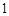 为公差的等差数列.………………..4分
为公差的等差数列.………………..4分
⑵由⑴可知, ,即
,即 ,
,
∴当 时,
时, ,
,
当 时,
时,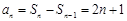 ,
,
经检验,当 时也成立,∴
时也成立,∴ .
.
于是 .
.
∵ ,
,
∴ ,
,
相减,解得: .……………………8分
.……………………8分
⑶∵ ,
,
∴

 .………………….12分
.………………….12分
考点:本试题考查了等差数列和等比数列的概念,以及数列求和。
点评:解决该试题的关键是对于等差数列和等比数列的通项公式的熟练表示和求解,注意对于已知和式求解通项公式的时候,要注意对于首项的验证,这个是易错点。同时要掌握错位相减法求和,属于中档题。


科目:高中数学 来源: 题型:解答题
已知数列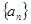 中,
中, 且点
且点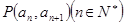 在直线
在直线 上。
上。
(1)求数列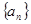 的通项公式;
的通项公式; (2)
(2)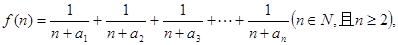 求函数
求函数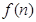 的最小值;
的最小值;
(3)设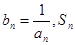 表示数列
表示数列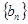 的前
的前 项和。试问:是否存在关于
项和。试问:是否存在关于 的整式
的整式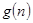 ,使得
,使得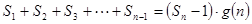 对于一切不小于2的自然数
对于一切不小于2的自然数 恒成立?若存在,写出
恒成立?若存在,写出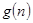 的解析式,并加以证明;若不存在,试说明理由。
的解析式,并加以证明;若不存在,试说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知数列 满足
满足 ,数列
,数列 满足
满足 ,
,
数列 满足
满足 .
.
(1)若 ,证明数列
,证明数列 为等比数列;
为等比数列;
(2)在(1)的条件下,求数列 的通项公式;
的通项公式;
(3)若 ,证明数列
,证明数列 的前
的前 项和
项和 满足
满足 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(13分)已知数列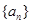 是公差为正的等差数列,其前
是公差为正的等差数列,其前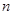 项和为
项和为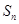 ,点
,点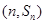 在抛物线
在抛物线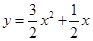 上;各项都为正数的等比数列
上;各项都为正数的等比数列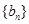 满足
满足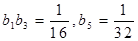 .
.
(1)求数列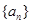 ,
,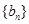 的通项公式;
的通项公式;
(2)记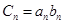 ,求数列
,求数列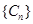 的前n项和
的前n项和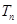 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com