
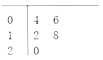
【题目】某县共有90间农村淘宝服务站,随机抽取5间,统计元旦期间的网购金额(单位:万元)的茎叶图如图所示,其中茎为十位数,叶为个位数.若网购金额(单位:万元)不小于18的服务站定义为优秀服务站,其余为非优秀服务站.从随机抽取的5间服务站中再任取2间作网购商品的调查,则恰有1间是优秀服务站的概率为_____.
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知
中,已知![]() ,
,![]() 为抛物线
为抛物线![]() :
:![]() 上两点,
上两点,![]() 为抛物线焦点.分别过
为抛物线焦点.分别过![]() ,
,![]() 作抛物线的切线交于点
作抛物线的切线交于点![]() .
.
(1)若![]() ,求
,求![]() ;
;
(2)若![]() ,
,![]() 分别交
分别交![]() 轴于
轴于![]() ,
,![]() 两点,试问
两点,试问![]() 的外接圆是否过定点?若是,求出该定点坐标,若不是,请说明理由.
的外接圆是否过定点?若是,求出该定点坐标,若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线的顶点为A,焦点为F.过F作直线l与抛物线交于点P、Q,直线AP、AQ分别与抛物线的准线交于点M、N.问:直线l满足什么条件时,三直线PN、QM、AF恒交于一点?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年春节期间,某超市准备举办一次有奖促销活动,若顾客一次消费达到400元则可参加一次抽奖活动,超市设计了两种抽奖方案.
方案一:一个不透明的盒子中装有30个质地均匀且大小相同的小球,其中10个红球,20个白球,搅拌均匀后,顾客从中随机抽取一个球,若抽到红球则顾客获得60元的返金券,若抽到白球则获得20元的返金券,且顾客有放回地抽取3次.
方案二:一个不透明的盒子中装有30个质地均匀且大小相同的小球,其中10个红球,20个白球,搅拌均匀后,顾客从中随机抽取一个球,若抽到红球则顾客获得80元的返金券,若抽到白球则未中奖,且顾客有放回地抽取3次.
(1)现有两位顾客均获得抽奖机会,且都按方案一抽奖,试求这两位顾客均获得180元返金券的概率;
(2)若某顾客获得抽奖机会.
①试分别计算他选择两种抽奖方案最终获得返金券的数学期望;
②为了吸引顾客消费,让顾客获得更多金额的返金券,该超市应选择哪一种抽奖方案进行促销活动?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,点
中,点![]() 在平面
在平面![]() 内运动,使得二面角
内运动,使得二面角![]() 的平面角与二面角
的平面角与二面角![]() 的平面角互余,则点
的平面角互余,则点![]() 的轨迹是( )
的轨迹是( )

A. 一段圆弧 B. 椭圆的一部分 C. 抛物线 D. 双曲线的一支
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 在左、右焦点分别为
在左、右焦点分别为![]() ,
,![]() ,动点
,动点![]() 在椭圆
在椭圆![]() 上,
上,![]() 的周长为6,且面积的最大值为
的周长为6,且面积的最大值为![]() .
.
(1)求![]() 的方程;
的方程;
(2)设直线![]() 与
与![]() 的另一个交点为
的另一个交点为![]() ,过
,过![]() ,
,![]() 分别作直线
分别作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,
,![]() ,
,![]() 与
与![]() 轴的交点为
轴的交点为![]() .若
.若![]() ,
,![]() ,
,![]() 的面积成等差数列,求直线
的面积成等差数列,求直线![]() 斜率的取值范围.
斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A.已知随机变量![]() ,若
,若![]() .则
.则![]()
B.已知分类变量![]() 与
与![]() 的随机变量
的随机变量![]() 的观察值为
的观察值为![]() ,则当
,则当![]() 的值越大时,“
的值越大时,“![]() 与
与![]() 有关”的可信度越小.
有关”的可信度越小.
C.在线性回归模型中,计算其相关指数![]() ,则可以理解为:解析变量对预报变量的贡献率约为
,则可以理解为:解析变量对预报变量的贡献率约为![]()
D.若对于变量![]() 与
与![]() 的
的![]() 组统计数据的线性回归模型中,相关指数
组统计数据的线性回归模型中,相关指数![]() .又知残差平方和为
.又知残差平方和为![]() .那么
.那么![]() .(注意:
.(注意: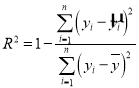 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,天花板上挂着3串玻璃球,射击玻璃球规则:每次击中1球,每串中下面球没击中,上面球不能击中,则把这6个球全部击中射击方法数是( )
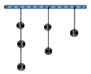
A.78B.60C.48D.36
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com