练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

     如图,正三棱锥,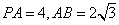，D为BC的中点， E为AP的中点．P在底面△ABC内的射影为O，以O为坐标原点，OD、OP所在直线分别为Y、Z轴建立如图所示的空间直角坐标系O—XYZ．

    ⑴ 写出点A、B、D、E的坐标；

    ⑵ 用向量法求异面直线AD与BE所成的角．

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

    【答案】

     解：⑴易知O为正三角形的中心，并且，AD⊥BC， BC//OX．

    故.

    ∴------４分

    ⑵ ∵，------6分

    ∴．------8分

    故异面直线AD与BE所成的角为．------10分

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网如图，正三棱锥S-ABC中，侧面SAB与底面ABC所成的二面角等于α，动点P在侧面SAB内，PQ⊥底面ABC，垂足为Q，PQ=PS•sinα，则动点P的轨迹为（　　）
    A、线段B、圆C、一段圆弧D、一段抛物线

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    9、如图，正三棱锥SABC的侧棱与底面边长相等，如果E、F分别为SC、AB的中点，那么异面直线EF与SA所成的角等于（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    精英家教网如图，正三棱锥S-ABC的侧面是边长为a的正三角形，D是SA的中点，E是BC的中点，求△SDE绕直线SE旋转一周所得到的旋转体的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    精英家教网如图，正三棱锥P-ABC的底面边长为1，E，F，G，H，分别是PA，AC，BC，PD的中点，四边形EFGH的面积为S（x），则S（x）值域为_________（　　）
    A、{
    1
    4
    }
    B、（
    		3
    12
    ，+∞）
    C、（0，+∞）
    D、（
    		3
    6
    ，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

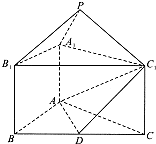    如图，正三棱锥ABC-A1B1C1中，AB=2，AA1=1，D是BC的中点，点P在平面BCC1B1内，PB1=PC1=
    		2
    ．
    （I）求证：PA1⊥B1C1；
    （II）求证：PB1∥平面AC1D；
    （III）求多面体PA1B1DAC1的体积．

    查看答案和解析>>

    同步练习册答案