
如图,三棱锥P-ABC中,PC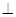 平面ABC,PC=AC=2, AB=BC,D是PB上一点,且CD
平面ABC,PC=AC=2, AB=BC,D是PB上一点,且CD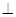 平面PAB
平面PAB

(1)求证:AB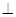 平面PCB;
平面PCB;
(2)求异面直线AP与BC所成角的大小;
(3)求二面角C-PA-B 的大小的余弦值。
(1)根据题意,由于PC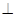 平面ABC,AB
平面ABC,AB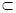 平面ABC,
平面ABC,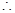 PC
PC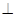 AB,同时
AB,同时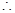 CD
CD 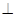 AB,然后得证明。
AB,然后得证明。
(2)建立空间直角坐标系来分析平面的法向量以及直线 方向向量来求解线面角
(3) 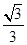
【解析】
试题分析:解:(1)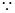 PC
PC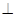 平面ABC,AB
平面ABC,AB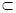 平面ABC,
平面ABC,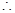 PC
PC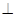 AB,
AB,
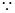 CD
CD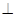 平面PAB,AB
平面PAB,AB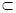 平面PAB,
平面PAB,
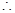 CD
CD 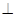 AB。又
AB。又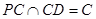 ,
,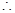 AB
AB 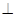 平面PCB
平面PCB
(2)由(1)AB 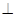 平面PCB ,
平面PCB ,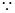 PC=AC=2, 又
PC=AC=2, 又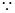 AB=BC,
可求得BC=
AB=BC,
可求得BC= 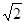
以B为原点,如图建立空间直角坐标系,
则A(0,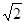 ,0),B(0,0,0), C(
,0),B(0,0,0), C(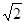 ,0,0) P(
,0,0) P(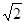 ,0,2)
,0,2)
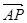 =(
=(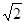 ,-
,-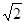 ,2),
,2),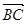 =(
=(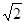 ,0,0) 则
,0,0) 则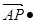
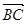 =
=
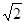 +0+0=2
+0+0=2
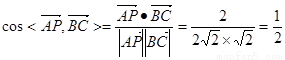
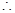 异面直线AP与BC所成的角为
异面直线AP与BC所成的角为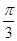
(3)设平面PAB的法向量为m=(x,y,z)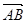 =(0,-
=(0,-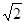 ,0),
,0),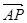 =(
=(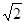 ,
,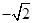 ,2)
,2)
则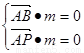 ,即,得m=(
,即,得m=(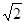 ,0,-1)设平面PAC的法向量为n=(x,y,z)
,0,-1)设平面PAC的法向量为n=(x,y,z)
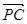 =(0,0,-2),
=(0,0,-2),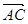 =(
=(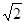 ,-
,-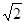 ,0),则
,0),则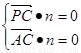
得n=(1,1,0)cos<m,n>=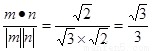
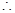 二面角C-PA-B大小的余弦值为
二面角C-PA-B大小的余弦值为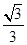
考点:空间中点线面 位置关系的运用
点评:解决该试题的关键是能熟练的运用线面垂直判定定理来证明,以及向量法求解角的问题,属于基础题。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 如图,三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB
如图,三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB查看答案和解析>>
科目:高中数学 来源: 题型:
 (2006•石景山区一模)如图,三棱锥P-ABC中,
(2006•石景山区一模)如图,三棱锥P-ABC中,| PA |
| AB |
| PA |
| AC |
| AB |
| AC |
| PA |
| AC |
| AB |
|
| ||
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•湖南模拟)如图,三棱锥P-ABC中,侧面PAC⊥底面ABC,∠APC=90°,且AB=4,AP=PC=2,BC=2
(2012•湖南模拟)如图,三棱锥P-ABC中,侧面PAC⊥底面ABC,∠APC=90°,且AB=4,AP=PC=2,BC=2| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•德阳二模)如图,三棱锥P-ABC中,PA丄面ABC,∠ABC=90°,PA=AB=1,BC=2,则P-ABC的外接球的表面积为
(2012•德阳二模)如图,三棱锥P-ABC中,PA丄面ABC,∠ABC=90°,PA=AB=1,BC=2,则P-ABC的外接球的表面积为查看答案和解析>>
科目:高中数学 来源: 题型:
 如图在三棱锥P-ABC中,AB⊥PC,AC=2,BC=4,AB=2
如图在三棱锥P-ABC中,AB⊥PC,AC=2,BC=4,AB=2| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com