
(��������14��)
��ijѧУ��һ�꼶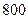 ��ѧ���������ȡ
��ѧ���������ȡ ���������ߣ��ݲ�������ȡ��ѧ��������ȫ������
���������ߣ��ݲ�������ȡ��ѧ��������ȫ������ ��
��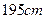 ֮�䣬��������������·�ʽ�ֳɰ��飺��һ��
֮�䣬��������������·�ʽ�ֳɰ��飺��һ�� ���ڶ���
���ڶ���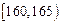 �����ڰ���
�����ڰ���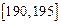 ����ͼ
����ͼ
�ǰ��������鷽���õ�������ͼ�� 

(1)������֪������д�������
| �顡�� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| ������ | | | |  | | | | |
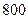 ��ѧ����������
��ѧ���������� ����(��
����(�� )��������
)�������� ��Ϊ����������ΪŮ������������
��Ϊ����������ΪŮ������������ ��ΪŮ��������Ϊ�������ڵڶ���͵������и�ѡһ��ͬѧ���ʵ��С�飬�ʣ�ʵ��С����ǡΪһ��һŮ�ĸ����Ƕ��٣�
��ΪŮ��������Ϊ�������ڵڶ���͵������и�ѡһ��ͬѧ���ʵ��С�飬�ʣ�ʵ��С����ǡΪһ��һŮ�ĸ����Ƕ��٣� �⣺��1��������ͼ�õ�����Ƶ��Ϊ
��Ŀ��������ѧ
��Դ��
���ͣ�
��Ŀ��������ѧ
��Դ��
���ͣ�
����С������14�֣�����ԲC1�ķ���Ϊ
��Ŀ��������ѧ
��Դ��2011�꽭��ʡ�����н����Ҹ߶���ѧ����ĩ��ѧ������A��
���ͣ������
����С������14�֣�
��Ŀ��������ѧ
��Դ��2015��ɽ��ʡ�����и�һ��ѧ����ĩ������ѧ�Ծ��������棩
���ͣ������
(��С������14��) ij�����һӦ����Ʒ��ȥ20������ۼ۸������������˼��ͳ�Ʒ��֣��� ����д�����۶� ���������Ʒ��7������� ������Ʒ�ڼ���������������������.
��Ŀ��������ѧ
��Դ��2011-2012ѧ��㶫ʡ������ѧ�ڵ�һ���¿��Ŀ���ѧ�Ծ��������棩
���ͣ������
����С������14�֣���֪ �� �� �� �� �� ֤����
����ѧУ��ѡ - ��ϰ���б� - �����б� ����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��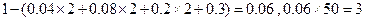 ��
��
������������Ϊ3�ˣ� ���������������������������������������� 1����� 1 2 3 4 5 6 7 8 ���������� 2 4 10 10 15 4 3 2  �������������������������� 4��
�������������������������� 4��
��2���⣺������ͼ��ǰ����Ƶ��Ϊ(0.008+0.016+0.04+0.04+0.06)�� 5=0.82��������Ƶ��Ϊ1-0.82=0.18��
5=0.82��������Ƶ��Ϊ1-0.82=0.18��
��������ѧУ�����꼶������180cm����(��180cm)������800��0.18=144(��)�� ���� 8��
��3���ڶ����� �˼�Ϊ
�˼�Ϊ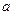 ��
��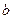 ��
��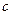 ��
��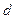 ������aΪ������b��c��dΪŮ�������������˼�Ϊ1��2��3��
������aΪ������b��c��dΪŮ�������������˼�Ϊ1��2��3��
����1��2Ϊ������3ΪŮ���������¼��б����£� ������������������������������ 9��[��Դ:Z_xx_k.Com] a B c d 1 1a 1b 1c 1d 2 ����


�ο����뵥Ԫ����ϵ�д�
���ͽ��С��ʿ��Ԫ��ĩһ��ͨϵ�д�
��Ԫ����AB��̨��������ϵ�д�
�Ƹ���˼ά���ſ�����Ԫ����ĩ��ϵ�д�
��У��ʦ��ڽ��ϵ�д�
СѧӢ���ʱ��ϵ�д�
�����°���ϵ�д�


������ҵ��������������ϵ�д�

�꼶
���пγ�
�꼶
���пγ�
��һ
��һ��ѿγ��Ƽ���
��һ
��һ��ѿγ��Ƽ���
�߶�
�߶���ѿγ��Ƽ���
����
������ѿγ��Ƽ���
����
������ѿγ��Ƽ���
����
������ѿγ��Ƽ���
sin2x+2sin(3
+x)cos(�� 4
+x)���� 4
��I������f��x���ı���ʽ������f��x������С�����ڣ�
��II����x��[0��
] ʱ������f(x)��ֵ���� 2 ![]() (a��b��0)������C2�ķ���Ϊy=
(a��b��0)������C2�ķ���Ϊy=![]() ��������C1��C2�ڵ�һ������ֻ��һ��������P����1������a��ʾ��P�����ꣻ��2����A��B����ԲC1���������㣬��a�仯ʱ�����ABP���������S(a)��ֵ��3����min{y1,y2,����,yn}Ϊy1,y2,����,yn����С��һ������g(a)������ԲC1�İ뽹��Ϊ�߳��������ε������������f(a)=min{g(a), S(a)}�ı���ʽ��
��������C1��C2�ڵ�һ������ֻ��һ��������P����1������a��ʾ��P�����ꣻ��2����A��B����ԲC1���������㣬��a�仯ʱ�����ABP���������S(a)��ֵ��3����min{y1,y2,����,yn}Ϊy1,y2,����,yn����С��һ������g(a)������ԲC1�İ뽹��Ϊ�߳��������ε������������f(a)=min{g(a), S(a)}�ı���ʽ��
��֪ =2���㣨
=2���㣨 ���ں���
���ں��� ��ͼ���ϣ�����
��ͼ���ϣ����� =
= .
.
(1)֤�������� }�ǵȱ����У�
}�ǵȱ����У�
��2���� ����
���� ������{
������{ }��ͨ�ʽ��
}��ͨ�ʽ��
��3���� ��������{
��������{ }��ǰn���
}��ǰn��� ����֤��
����֤�� .
. ��(
��( )�����ۼ۸�(��λ��Ԫ)Ϊ
)�����ۼ۸�(��λ��Ԫ)Ϊ ����
���� ���������Ϊ
���������Ϊ ����֪����Ʒ�ɱ�Ϊÿ��25Ԫ.
����֪����Ʒ�ɱ�Ϊÿ��25Ԫ. ���ڵ�
���ڵ� ��ĺ�����ϵʽ��
��ĺ�����ϵʽ�� ��ͼ���ڵ�
��ͼ���ڵ� ����������ֱ��
����������ֱ�� ƽ��.
ƽ��. ��
�� ����Ĺ�ϵʽ��
����Ĺ�ϵʽ�� �Ϻ��������
�Ϻ�������� ��ȡֵ��Χ��
��ȡֵ��Χ�� ��
�� ��
��
��Ȩ��������վ�������£�ͼƬ��Դ�����磬����Ȩ����Ȩ��ԭ�������У�ת�������ַ���Ȩ��������Ȩ����������������֪�����ǽ����촦������ϵqq��3310059649��
ICP�������: ��ICP��07509807��-10 ����������42018502000812��