
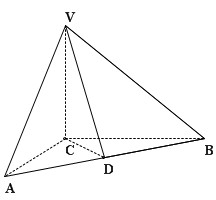
如图,在三棱锥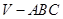 中,
中,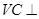 底面
底面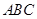 ,
, 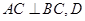 为
为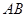 的中点,
的中点,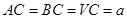 .
.
(1)求证: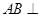 平面
平面 ;
;
(2)求点 到平面
到平面 的距离。
的距离。
(1)证明过程详见解析;(2)点 到平面
到平面 的距离为
的距离为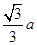 .
.
解析试题分析:本题以三棱锥为几何背景考查线面垂直的判断和点到面的距离的求法,可以运用传统几何法求解,突出考查空间想象能力和计算能力.第一问,先利用线面垂直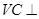 平面
平面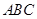 ,得到线线垂直
,得到线线垂直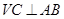 ,由等腰三角形,得
,由等腰三角形,得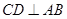 ,由上述两个条件得
,由上述两个条件得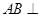 平面
平面 ;第二问,利用第一问可得面
;第二问,利用第一问可得面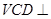 面
面 ,利用面面垂直的性质,得
,利用面面垂直的性质,得 到
到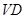 的距离即为
的距离即为 到面
到面 的距离,在直角三角形
的距离,在直角三角形 中,用等面积法表示
中,用等面积法表示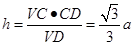 .法二:第二问,等体积法求点面距离,
.法二:第二问,等体积法求点面距离, ,即
,即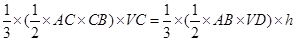 ,得
,得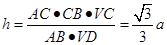 .
.
试题解析:(1)因为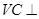 平面
平面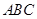 ,
, 平面
平面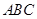 ,
,
所以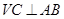 2分
2分
又因为在 中,
中,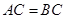 ,
,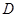 为
为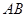 的中点,
的中点,
所以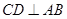 4分
4分
又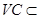 平面
平面 ,
,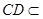 平面
平面 ,且
,且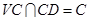 ,
,
所以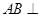 平面
平面 6分
6分
(2)法一:因为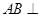 平面
平面 且
且 平面
平面
所以平面
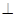 平面
平面 , 8分
, 8分
又因为平面
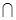 平面
平面
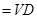 ,
,
所以点 到
到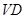 的距离
的距离 即为点
即为点 到平面
到平面 的距离, 10分
的距离, 10分
在直角三角形 中,由
中,由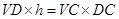 11分
11分
得 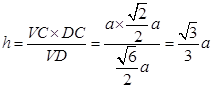 13分
13分
所以点 到平面
到平面 的距离为
的距离为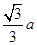 . 14分
. 14分
法二:设点 到平面
到平面 的距离为
的距离为 , 据
, 据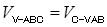 8分
8分
即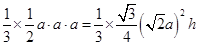 ,得
,得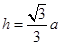 13分
13分
所以点 到平面
到平面 的距离为
的距离为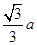 . 14分
. 14分
考点:1.线面垂直的判定定理;2.面面垂直的性质;3.等体


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
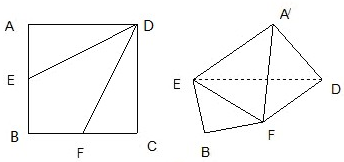
如图,边长为2的正方形ABCD,E,F分别是AB,BC的中点,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于 .
.
(1)求证: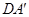 ⊥EF;
⊥EF;
(2)求二面角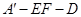 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
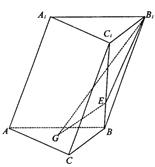
如图,在斜三棱柱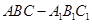 中,侧面
中,侧面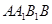 ⊥底面
⊥底面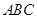 ,侧棱
,侧棱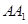 与底面
与底面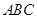 成
成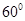 的角,
的角,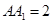 .底面
.底面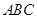 是边长为2的正三角形,其重心为
是边长为2的正三角形,其重心为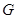 点,
点,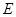 是线段
是线段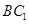 上一点,且
上一点,且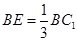 .
.
(Ⅰ)求证: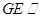 //侧面
//侧面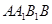 ;
;
(Ⅱ)求平面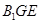 与底面
与底面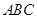 所成锐二面角的正切值.
所成锐二面角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在四棱锥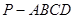 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱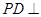 底面ABCD,
底面ABCD,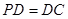 ,E是PC的中点.
,E是PC的中点.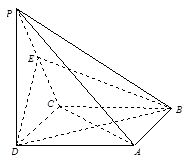
(Ⅰ)证明 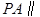 平面EDB;
平面EDB;
(Ⅱ)求EB与底面ABCD所成的角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=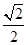 AB.
AB.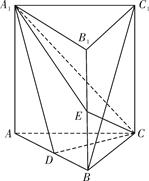
(Ⅰ)证明:BC1∥平面A1CD;
(Ⅱ)求二面角D-A1C-E的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com