
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,且椭圆上存在一点
,且椭圆上存在一点![]() ,满足
,满足![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过椭圆![]() 右焦点
右焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,求
,求![]() 的内切圆的半径的最大值.
的内切圆的半径的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)利用余弦定理和椭圆的定义即可求出a,再根据b2=a2﹣c2=3,可得椭圆的方程;(2)设A(x1,y1),B(x2,y2),设△F1AB的内切圆的半径为R,表示出△F1AB的周长与面积,设直线l的方程为x=my+1,联立直线与椭圆方程,利用韦达定理,表示三角形面积,令t![]() ,利用函数的单调性求解面积的最大值,然后求解△F1AB内切圆半径的最大值为
,利用函数的单调性求解面积的最大值,然后求解△F1AB内切圆半径的最大值为![]() .
.
(1)设![]() ,则
,则![]() 内,
内,
由余弦定理得![]() ,化简得
,化简得![]() ,解得
,解得![]()
故![]() ,得
,得![]()
所以椭圆![]() 的标准方程为
的标准方程为![]()
(2)设![]() ,设
,设![]() 得内切圆半径为
得内切圆半径为![]()
![]() 的周长为
的周长为![]()
所以![]()
根据题意知,直线![]() 的斜率不为零,可设直线
的斜率不为零,可设直线![]() 的方程为
的方程为![]()
由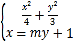 得
得![]()
![]()
由韦达定理得![]()
![]()
![]()
令![]() ,则
,则![]()
令![]() ,则
,则![]() 时,
时,![]() 单调递增,
单调递增,
![]()
即当![]() 时,
时,![]() 的最大值为
的最大值为![]() ,此时
,此时![]() .
.
故当直线![]() 的方程为
的方程为![]() 时,
时,![]() 内圆半径的最大值为
内圆半径的最大值为![]() .
.


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:
【题目】在梯形![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,线段
的中点,线段![]() 与
与![]() 交于
交于![]() 点(如图1).将
点(如图1).将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使得二面角
的位置,使得二面角![]() 为直二面角(如图2).
为直二面角(如图2).
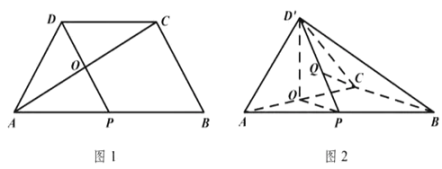
(1)求证:![]() 平面
平面![]() ;
;
(2)线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市收集并整理了该市2017年1月份至10月份每月份最低气温与最高气温(单位:![]() )的数据,绘制了折线图(如图).已知该市每月的最低气温与当月的最高气温两变量具有较好的线性关系,则根据该折线图,下列结论错误的是()
)的数据,绘制了折线图(如图).已知该市每月的最低气温与当月的最高气温两变量具有较好的线性关系,则根据该折线图,下列结论错误的是()
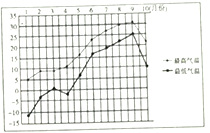
A. 最低气温低于![]() 的月份有
的月份有![]() 个
个
B. ![]() 月份的最高气温不低于
月份的最高气温不低于![]() 月份的最高气温
月份的最高气温
C. 月温差(最高气温减最低气温)的最大值出现在![]() 月份
月份
D. 每月份最低气温与当月的最高气温两变量为正相关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)若![]() 是从0,1,2,3,4五个数中任取的一个数,
是从0,1,2,3,4五个数中任取的一个数,![]() 是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
(2)若![]() 是从区间
是从区间![]() 上任取的一个数,
上任取的一个数,![]() 是从区间
是从区间![]() 上任取的一个数,求上述方程有实根的概率.
上任取的一个数,求上述方程有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新个税法于2019年1月1日进行实施.为了调查国企员工对新个税法的满意程度,研究人员在![]() 地各个国企中随机抽取了1000名员工进行调查,并将满意程度以分数的形式统计成如下的频率分布直方图,其中
地各个国企中随机抽取了1000名员工进行调查,并将满意程度以分数的形式统计成如下的频率分布直方图,其中![]() .
.
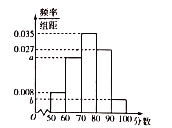
(1)求![]() 的值并估计被调查的员工的满意程度的中位数;(计算结果保留两位小数)
的值并估计被调查的员工的满意程度的中位数;(计算结果保留两位小数)
(2)若按照分层抽样从![]() ,
,![]() 中随机抽取8人,再从这8人中随机抽取2人,求至少有1人的分数在
中随机抽取8人,再从这8人中随机抽取2人,求至少有1人的分数在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,错误的是( )
A.圆锥所有的轴截面是全等的等腰三角形
B.圆柱的轴截面是过母线的截面中面积最大的一个
C.圆锥的轴截面是所有过顶点的界面中面积最大的一个
D.当球心到平面的距离小于球面半径时,球面与平面的交线总是一个圆
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新个税法于2019年1月1日进行实施.为了调查国企员工对新个税法的满意程度,研究人员在![]() 地各个国企中随机抽取了1000名员工进行调查,并将满意程度以分数的形式统计成如下的频率分布直方图,其中
地各个国企中随机抽取了1000名员工进行调查,并将满意程度以分数的形式统计成如下的频率分布直方图,其中![]() .
.
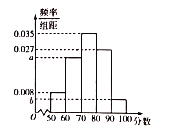
(1)求![]() 的值并估计被调查的员工的满意程度的中位数;(计算结果保留两位小数)
的值并估计被调查的员工的满意程度的中位数;(计算结果保留两位小数)
(2)若按照分层抽样从![]() ,
,![]() 中随机抽取8人,再从这8人中随机抽取2人,求至少有1人的分数在
中随机抽取8人,再从这8人中随机抽取2人,求至少有1人的分数在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,椭圆短轴的一个端点与两个焦点构成的三角形的面积为
,椭圆短轴的一个端点与两个焦点构成的三角形的面积为![]() ,直线l的方程为:
,直线l的方程为:![]()
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)已知直线l与椭圆![]() 相交于
相交于![]() 、
、![]() 两点
两点
①若线段![]() 中点的横坐标为
中点的横坐标为![]() ,求斜率
,求斜率![]() 的值;
的值;
②已知点![]() ,求证:
,求证:![]() 为定值
为定值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com