
分析 设存在x0<0(x0≠-1),满足f(x0)=0,推出这矛盾,问题得以解决
解答 证明:设存在x0<0(x0≠-1),满足f(x0)=0,--------------------------------------(2分)
则${a^{x_0}}=-\frac{{{x_0}-2}}{{{x_0}+1}}$.
又0<${a^{x_0}}$<1,所以0<-$\frac{{x}_{0}-2}{{x}_{0}+1}$<1,--------------------------------------------(4分)
解之得:$\frac{1}{2}<{x_0}<2$,---------------------------------------------------(8分)
与x0<0(x0≠-1)假设矛盾.
故f(x)=0没有负实数根.------------------------------------------------(10分)
点评 本题考查用反证法证明数学命题,推出矛盾,是解题的关键和难点.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
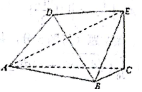 如图,以A、B、C、D、E为顶点的六面体中,△ABC和△ABD均为等边三角形,且平面ABC⊥平面ABD,EC⊥平面ABC,EC=$\sqrt{3}$,AB=2.
如图,以A、B、C、D、E为顶点的六面体中,△ABC和△ABD均为等边三角形,且平面ABC⊥平面ABD,EC⊥平面ABC,EC=$\sqrt{3}$,AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{π}{3}$+$\frac{2kπ}{3}$,$\frac{π}{2}$+$\frac{2kπ}{3}$](k∈Z) | B. | [-$\frac{π}{3}$+$\frac{4kπ}{3}$,$\frac{π}{2}$+$\frac{4kπ}{3}$](k∈Z) | ||
| C. | [-$\frac{π}{6}$+$\frac{2kπ}{3}$,$\frac{π}{2}$+$\frac{2kπ}{3}$](k∈Z) | D. | [-$\frac{π}{6}$+$\frac{4kπ}{3}$,$\frac{π}{2}$+$\frac{4kπ}{3}$](k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com