
分析 由数列{an}为等比数列且a5•a2n-5=22n(n≥3),可得$a_n^2={2^{2n}}$,又an>0,可得an.再利用对数的运算性质、等差数列的求和公式即可得出.
解答 解:由数列{an}为等比数列且a5•a2n-5=22n(n≥3),可得$a_n^2={2^{2n}}$,
又an>0,所以${a_n}={2^n}$.
则${S_n}={log_2}{a_1}+{log_2}{a_2}+…+{log_2}{a_n}={log_2}({a_1}{a_2}…{a_n})={log_2}{2^{1+2+…+n}}$
=1+2+…+n=$\frac{n(n+1)}{2}$.
点评 本题考查了等差数列与等比数列的通项公式与求和公式及其性质,考查了推理能力与计算能力,属于中档题.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:解答题
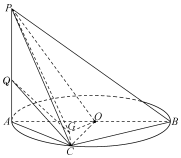 如图,点C在以AB为直径的圆O上,PA垂直与圆O所在平面,G为△AOC的垂心.
如图,点C在以AB为直径的圆O上,PA垂直与圆O所在平面,G为△AOC的垂心.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{4}$,+∞) | B. | (2,+∞) | C. | (-∞,2) | D. | (-1,$\frac{1}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9π}{2}$ | B. | $\frac{125π}{6}$ | C. | $\frac{32π}{3}$ | D. | 36π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com