
【题目】已知a,b,c分别为△ABC内角A,B,C的对边, ![]() .
.
(Ⅰ)求角B的大小;
(Ⅱ)若△ABC边AC上的高h=b,求 ![]() 的值.
的值.
【答案】解:(Ⅰ)由 ![]() . 根据正弦定理,可得:
. 根据正弦定理,可得: ![]() ,
,
即a﹣bcosC=csinB,
得:sinA﹣sinBcosC=sinCsinB.
B+C+A=π
∴sinA=sin(B+C)
∴sinBcosC+sinCcosB﹣sinBcosC=sinCsinB.
可得:sinCcosB=sinCsinB.
∵0<C<π,sinC≠0.
∴cosB=sinB
∵0<B<π.
∴B= ![]() .
.
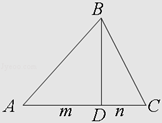
(Ⅱ)由题意,过B点作AC的高h=DB=b.设AD=m,DC=n,n+m=b.
则tanA= ![]() ,tanC=
,tanC= ![]() ,
,
可得 ![]() =sinB(
=sinB( ![]() )=sinB=
)=sinB= ![]() .
.
【解析】(Ⅰ)运用正弦定理结合三角形的内角和定理.即可得到A.(Ⅱ)根据△ABC边AC上的高h=b,求出tanA和tanC,带入化简可得答案.
【考点精析】关于本题考查的正弦定理的定义,需要了解正弦定理:![]() 才能得出正确答案.
才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设复数z1=(a2-4sin2θ)+(1+2cos θ)i,a∈R,θ∈(0,π),z2在复平面内对应的点在第一象限,且z=-3+4i.
(1)求z2及|z2|.
(2)若z1=z2,求θ与a2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中社团进行社会实践,对![]() 岁的人群随机抽取n人进行了一次是否开通“微博”的调查,若开通“微博”的称为“时尚族”,否则称为“非时尚族”,通过调查分别得到如图所示统计表和各年龄段人数频率分布直方图:
岁的人群随机抽取n人进行了一次是否开通“微博”的调查,若开通“微博”的称为“时尚族”,否则称为“非时尚族”,通过调查分别得到如图所示统计表和各年龄段人数频率分布直方图:
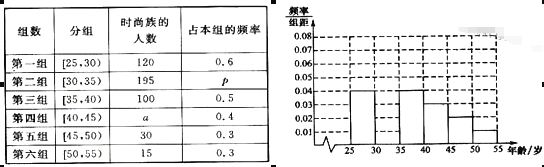
完成以下问题:
(Ⅰ)补全频率分布直方图并求![]() 的值;
的值;
(Ⅱ)从![]() 岁年龄段的“时尚族”中采用分层抽样法抽取
岁年龄段的“时尚族”中采用分层抽样法抽取![]() 人参加网络时尚达人大赛,其中选取
人参加网络时尚达人大赛,其中选取![]() 人作为领队,记选取的
人作为领队,记选取的![]() 名领队中年龄在
名领队中年龄在![]() 岁的人数为
岁的人数为![]() ,求
,求![]() 的分布列
的分布列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数f(x)=a+ ![]() (a,b∈R)有最大值和最小值,且最大值与最小值之和为6,则3a﹣2b=( )
(a,b∈R)有最大值和最小值,且最大值与最小值之和为6,则3a﹣2b=( )
A.7
B.8
C.9
D.10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的离心率为
的离心率为 ![]() ,左右焦点分别为F1 , F2 , 以椭圆短轴为直径的圆与直线
,左右焦点分别为F1 , F2 , 以椭圆短轴为直径的圆与直线 ![]() 相切.
相切.
(Ⅰ)求椭圆E的方程;
(Ⅱ)过点F1、斜率为k1的直线l1与椭圆E交于A,B两点,过点F2、斜率为k2的直线l2与椭圆E交于C,D两点,且直线l1 , l2相交于点P,若直线OA,OB,OC,OD的斜率kOA , kOB , kOC , kOD满足kOA+kOB=kOC+kOD , 求证:动点P在定椭圆上,并求出此椭圆方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() ax2-ln x,a∈R.
ax2-ln x,a∈R.
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程.
(2)讨论f(x)的单调性.
(3)是否存在a,使得方程f(x)=2有两个不等的实数根?若存在,求出a的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先阅读下列题目的证法,再解决后面的问题.
已知a1,a2∈R,且a1+a2=1,求证:a+a≥![]() .
.
证明:构造函数f(x)=(x-a1)2+(x-a2)2,则f(x)=2x2-2(a1+a2)x+a+a=2x2-2x+a+a.
因为对一切x∈R,恒有f(x)≥0,
所以Δ=4-8(a+a)≤0,从而得a+a≥![]() .
.
(1)若a1,a2,…,an∈R,a1+a2+…+an=1,请由上述结论写出关于a1,a2,…,an的推广式;
(2)参考上述证法,请对你推广的结论加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
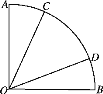
【题目】如图所示,在圆心角为90°的扇形AOB中,以圆心O作为起点作射线OC,OD,则使∠AOC+∠BOD<45°的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(1,2),
=(1,2), ![]() =(﹣2,m),
=(﹣2,m), ![]() =
= ![]() +(t2+1)
+(t2+1) ![]() ,
, ![]() =﹣k
=﹣k ![]() +
+ ![]()
![]() ,m∈R,k、t为正实数.
,m∈R,k、t为正实数.
(1)若 ![]() ∥
∥ ![]() ,求m的值;
,求m的值;
(2)若 ![]() ⊥
⊥ ![]() ,求m的值;
,求m的值;
(3)当m=1时,若 ![]() ⊥
⊥ ![]() ,求k的最小值.
,求k的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com