
【题目】已知向量 ![]() =(1,2),
=(1,2), ![]() =(﹣2,m),
=(﹣2,m), ![]() =
= ![]() +(t2+1)
+(t2+1) ![]() ,
, ![]() =﹣k
=﹣k ![]() +
+ ![]()
![]() ,m∈R,k、t为正实数.
,m∈R,k、t为正实数.
(1)若 ![]() ∥
∥ ![]() ,求m的值;
,求m的值;
(2)若 ![]() ⊥
⊥ ![]() ,求m的值;
,求m的值;
(3)当m=1时,若 ![]() ⊥
⊥ ![]() ,求k的最小值.
,求k的最小值.
【答案】
(1)解:由 ![]() ∥
∥ ![]() 可得1×m﹣2×(﹣2)=0,解之可得m=﹣4
可得1×m﹣2×(﹣2)=0,解之可得m=﹣4
(2)解:由 ![]() ⊥
⊥ ![]() 可得1×(﹣2)+2×m=0,解之可得m=1
可得1×(﹣2)+2×m=0,解之可得m=1
(3)解:当m=1时, ![]() =(﹣2t2﹣1,t2+3),
=(﹣2t2﹣1,t2+3),
![]() =(
=( ![]() ,
, ![]() ),
),
由 ![]() ⊥
⊥ ![]() 可得(﹣2t2﹣1)(
可得(﹣2t2﹣1)( ![]() )+(t2+3)(
)+(t2+3)( ![]() )=0,
)=0,
化简可得 ![]() ,当且仅当t=1时取等号,
,当且仅当t=1时取等号,
故k的最小值为:2
【解析】(1)(2)由平行和垂直的条件分别可得关于m的方程,解之可得;(3)把m=1代入,分别可得向量 ![]() ,
, ![]() 的坐标,由垂直可得k,x的关系式,由基本不等式可得答案.
的坐标,由垂直可得k,x的关系式,由基本不等式可得答案.
【考点精析】根据题目的已知条件,利用数量积判断两个平面向量的垂直关系的相关知识可以得到问题的答案,需要掌握若平面![]() 的法向量为
的法向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,要证
,要证![]() ,只需证
,只需证![]() ,即证
,即证![]() ;即:两平面垂直
;即:两平面垂直![]() 两平面的法向量垂直.
两平面的法向量垂直.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣x2+bln(x+1)在[0,+∞)上单调递减,则b的取值范围( )
A.[0,+∞)
B.[﹣ ![]() ,+∞)
,+∞)
C.(﹣∞,0]
D.(﹣∞,﹣ ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(1)若函数f(x)在区间(a,a+ ![]() )(a>0)上存在极值点,求实数a的取值范围;
)(a>0)上存在极值点,求实数a的取值范围;
(2)当x≥1时,不等式f(x)≥ ![]() 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是正方形.点E是棱PC的中点,平面ABE与棱PD交于点F.
(Ⅰ)求证:AB∥EF;
(Ⅱ)若PA=AD,且平面PAD⊥平面ABCD,求证:AF⊥平面PCD.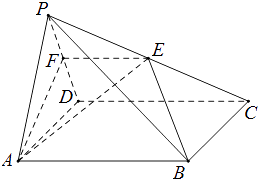
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,用四种不同颜色给图中的A,B,C,D,E,F六个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色,则不同的涂色方法有( )

A. 288种
B. 264种
C. 240种
D. 168种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com