
(09年长沙一中第八次月考理)(13分)若存在实常数![]() 和
和![]() ,使得函数
,使得函数![]() 和
和![]() 对其定义域上的任意实数
对其定义域上的任意实数![]() 分别满足:
分别满足:![]() 和
和![]() ,则称直线
,则称直线![]()
![]() 为
为![]() 和
和![]() 的“隔离直线”.已知
的“隔离直线”.已知![]() ,
,![]() (其中
(其中![]() 为自然对数的底数).
为自然对数的底数).
(Ⅰ)求![]() 的极值;
的极值;
解析:(Ⅰ) ![]()
![]() ,
,
![]() . …………………………2分
. …………………………2分
当![]() 时,
时,![]() . …………………………3分
. …………………………3分
![]() 当
当![]() 时,
时,![]() ,此时函数
,此时函数![]() 递减;
递减;
当![]() 时,
时,![]() ,此时函数
,此时函数![]() 递增;
递增;
∴当![]() 时,
时,![]() 取极小值,其极小值为
取极小值,其极小值为![]() . …………………………6分
. …………………………6分
(Ⅱ)解法一:由(Ⅰ)可知函数![]() 和
和![]() 的图象在
的图象在![]() 处有公共点,因此若存在
处有公共点,因此若存在![]() 和
和![]() 的隔离直线,则该直线过这个公共点. …………………………7分
的隔离直线,则该直线过这个公共点. …………………………7分
设隔离直线的斜率为![]() ,则直线方程为
,则直线方程为![]() ,即
,即
![]() . …………………………8分
. …………………………8分
由![]() ,可得
,可得![]() 当
当![]() 时恒成立.
时恒成立.
![]() ,
,
![]() 由
由![]() ,得
,得![]() . …………………………10分
. …………………………10分
下面证明![]() 当
当![]() 时恒成立.
时恒成立.
令![]()
![]() ,则
,则
![]() , …………………………11分
, …………………………11分
当![]() 时,
时,![]() .
.
![]() 当
当![]() 时,
时,![]() ,此时函数
,此时函数![]() 递增;
递增;
当![]() 时,
时,![]() ,此时函数
,此时函数![]() 递减;
递减;
∴当![]() 时,
时,![]() 取极大值,其极大值为
取极大值,其极大值为![]() .
.
从而![]() ,即
,即![]() 恒成立.………13分
恒成立.………13分
∴函数![]() 和
和![]() 存在唯一的隔离直线
存在唯一的隔离直线![]() . ………………………14分
. ………………………14分
解法二: 由(Ⅰ)可知当![]() 时,
时,![]() (当且当
(当且当![]() 时取等号) .……7分
时取等号) .……7分
若存在![]() 和
和![]() 的隔离直线,则存在实常数
的隔离直线,则存在实常数![]() 和
和![]() ,使得
,使得
![]() 和
和![]() 恒成立,
恒成立,
令![]() ,则
,则![]() 且
且![]()
![]() ,即
,即![]() . …………………………8分
. …………………………8分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
(09年长沙一中第八次月考理)(13分)已知直线L:x-y-3=0,抛物线C的顶点在原点,焦点在![]() 轴正半轴上,S是抛物线C上任意一点,T是直线L上任意一点,若|ST|的最小值为d>0时,点S的横坐标为2.
轴正半轴上,S是抛物线C上任意一点,T是直线L上任意一点,若|ST|的最小值为d>0时,点S的横坐标为2.
(1)求抛物线方程以及d的值;
(2)过抛物线C的对称轴上任一点![]() 作直线与抛物线交于
作直线与抛物线交于![]() 两点,点
两点,点![]() 是点
是点![]() 关于原点的对称点.设点
关于原点的对称点.设点![]() 分有向线段
分有向线段![]() 所成的比为
所成的比为![]() ,
,
证明:![]() ;
;
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年长沙一中第八次月考理)(本小题满分12分)如图,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EF//AC,∠CAF=∠AFE=90º,AB=![]() ,AF=FE=1.
,AF=FE=1.
(1)求证EC//平面BDF;
(2)求二面角A-DF-B的大小;
(3)试在线段AC上确定一点P,使得PF与BC所成的角是60°.
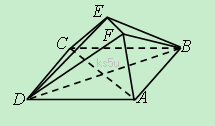
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年长沙一中第八次月考理)(本小题满分12分)我校文化体育艺术节的乒乓球决赛在甲乙两人中进行,比赛规则如下:比赛采用7局4胜制(先胜4局这获胜即比赛结束),在每一局比赛中,先得11分的一方为胜方;比赛没有平局,10平后,先连得2分的一方为胜方![]()
(1)根据以往战况,每局比赛甲胜乙的概率为0.6,设比赛的场数为![]() ,求
,求![]() 的分布列和期望;
的分布列和期望;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com