
【题目】设函数![]() .
.
(1)求![]() 的最小值;
的最小值;
(2)记![]() 的最小值为
的最小值为![]() ,已知函数
,已知函数![]() ,若对于任意的
,若对于任意的![]() ,恒有
,恒有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)求出函数![]() 的定义域,并利用导数研究其在定义域上的单调性,找到最小值点即可求得最小值;(2)
的定义域,并利用导数研究其在定义域上的单调性,找到最小值点即可求得最小值;(2)![]() ,把分子设为新函数
,把分子设为新函数![]() ,并用导数研究其单调性,可知
,并用导数研究其单调性,可知![]() 在
在![]() 上单调递增,由于
上单调递增,由于![]() ,且当
,且当![]() 时,
时,![]() ,所以存在
,所以存在![]() ,使
,使![]() ,且
,且![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,所以必有
上单调递增,所以必有![]() ,据此求得
,据此求得![]() ,分类参数即可求得参数
,分类参数即可求得参数![]() 的范围.
的范围.
试题解析:(1)由已知得![]() ..........1分
..........1分
令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]() ,
,
所以![]() 的单调减区间为
的单调减区间为![]() ,单调增区间为
,单调增区间为![]() ...................3分
...................3分
从而![]() ................4分
................4分
(2)由(1)中![]() 得
得![]() ................... 5分
................... 5分
所以![]() .............................6分
.............................6分
令![]() ,则
,则![]() ...................7分
...................7分
所以![]() 在
在![]() 上单调递增,
上单调递增,
因为![]() ,且当
,且当![]() 时,
时,![]() ,
,
所以存在![]() ,使
,使![]() ,且
,且![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增......8分
上单调递增......8分
因为![]() ,所以
,所以![]() ,即
,即![]() ,因为对于任意的
,因为对于任意的![]() ,恒有
,恒有![]() 成立,
成立,
所以![]() ............9分
............9分
所以![]() ,即
,即![]() ,亦即
,亦即![]() ,所以
,所以![]() ..................... 10分
..................... 10分
因为![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() ,从而
,从而![]() ,
,
所以![]() ,故
,故![]() .............................12分
.............................12分


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
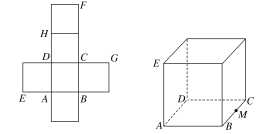
【题目】一个正方体的平面展开图及该正方体直观图的示意图如图所示,在正方体中,设BC的中点为M,GH的中点为N。
(1)请将字母F,G,H标记在正方体相应的顶点处(不需说明理由);
(2)证明:直线MN∥平面BDH;
(3)过点M,N,H的平面将正方体分割为两部分,求这两部分的体积比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点,长轴在
的中心在坐标原点,长轴在![]() 轴上,
轴上,![]() 分别在其左、右焦点,
分别在其左、右焦点,![]() 在椭圆上任意一点,且
在椭圆上任意一点,且![]() 的最大值为1,最小值为
的最大值为1,最小值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆
为椭圆![]() 的右顶点,直线
的右顶点,直线![]() 是与椭圆交于
是与椭圆交于![]() 两点的任意一条直线,若
两点的任意一条直线,若![]() ,证明直线
,证明直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知极点与直角坐标系的原点重合,极轴与![]() 轴的正半轴重合,圆
轴的正半轴重合,圆![]() 的极坐标方程是
的极坐标方程是![]() ,直线
,直线![]() 的参数方程是
的参数方程是 (
(![]() 为参数).
为参数).
(1)若![]() ,
, ![]() 为直线
为直线![]() 与
与![]() 轴的交点,
轴的交点, ![]() 是圆
是圆![]() 上一动点,求
上一动点,求![]() 的最大值;
的最大值;
(2)若直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com