
【题目】已知圆![]() ,直线
,直线![]() ,若直线
,若直线![]() 上存在点
上存在点![]() ,过点
,过点![]() 引圆的两条切线
引圆的两条切线![]() ,使得
,使得![]() ,则实数
,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B. [
B. [![]() ,
,![]() ]
]
C. ![]() D.
D. ![]() )
)
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】某火锅店为了了解气温对营业额的影响,随机记录了该店1月份其中5天的日营业额y(单位:万元)与该地当日最低气温x(单位:℃)的数据,如下表:
![]()
(1)求y关于x的线性回归方程![]() =
=![]() x+
x+![]() ;
;
(2)判断y与x之间是正相关还是负相关,若该地1月份某天的最低气温为6 ℃,用所求回归方程预测该店当日的营业额;
(3)设该地1月份的日最低气温X~N(μ,σ2),其中μ近似为样本平均数![]() ,σ2近似为样本方差s2,求P(3.8<X≤13.4).
,σ2近似为样本方差s2,求P(3.8<X≤13.4).
附:①回归方程![]() 中,
中,![]() =
=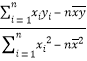 ,
,![]() =
=![]() ﹣
﹣![]() .
.
②![]() ≈3.2,
≈3.2,![]() ≈1.8.若X~N(μ,σ2),则P(μ-σ<X≤μ+σ)=0.682 7,P(μ-2σ<X≤μ+2σ)=0.954 5.
≈1.8.若X~N(μ,σ2),则P(μ-σ<X≤μ+σ)=0.682 7,P(μ-2σ<X≤μ+2σ)=0.954 5.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在航天员进行的一项太空实验中,要先后实施6个程序,其中程序![]() 只能出现在第一步或最后一步,程序
只能出现在第一步或最后一步,程序![]() 实施时必须相邻,请问实验顺序的编排方法共有 ( )
实施时必须相邻,请问实验顺序的编排方法共有 ( )
A. ![]() 种 B.
种 B. ![]() 种 C.
种 C. ![]() 种 D.
种 D. ![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面ABCD为平行四边形,PA⊥底面ABCD,
中,底面ABCD为平行四边形,PA⊥底面ABCD,![]() ,
,![]() ,
,![]() ,
,![]() .
.
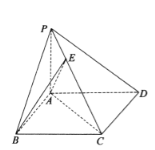
(1)求证:平面PCA⊥平面PCD;
(2)设E为侧棱PC上的一点,若直线BE与底面ABCD所成的角为45°,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() 两点,交圆
两点,交圆![]() 于
于![]() 两点(
两点(![]() 两点相邻).
两点相邻).
(Ⅰ)若![]() ,当
,当![]() 时,求
时,求![]() 的取值范围;
的取值范围;
(Ⅱ)过![]() 两点分别作曲线
两点分别作曲线![]() 的切线
的切线![]() ,两切线交于点
,两切线交于点![]() ,求
,求![]() 与
与![]() 面积之积的最小值.
面积之积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 经过点
经过点![]() ,离心率为
,离心率为![]() . 已知过点
. 已知过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点.
两点.

(1)求椭圆![]() 的方程;
的方程;
(2)试问![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值.若存在,求出点
为定值.若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为边长为2的菱形,
为边长为2的菱形,![]() ,
,![]() ,面
,面![]() 面
面![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.

(1)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 面
面![]() ,并说明理由;
,并说明理由;
(2)当二面角![]() 的余弦值为
的余弦值为![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成的角.
所成的角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() ’(
’(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 和
和![]() 的直角坐标方程;
的直角坐标方程;
(2)已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,且与曲线
,且与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com