
【题目】已知函数![]() .
.
(1)求函数![]() 的极值;
的极值;
(2)若不等式![]() 恒成立,求
恒成立,求![]() 的最小值(其中e为自然对数的底数).
的最小值(其中e为自然对数的底数).
【答案】(1)当![]() 时,
时,![]() 无极值;当
无极值;当![]() 时,
时,![]() 极大值为
极大值为![]() ,无极小值
,无极小值
(2)-1
【解析】
(1)求出导函数![]() ,确定函数单调性,得极值,需分类讨论.
,确定函数单调性,得极值,需分类讨论.
(2)![]() 恒成立,设
恒成立,设![]() ,求出
,求出![]() 的最大值
的最大值![]() ,由
,由![]() 得出
得出![]() 满足的不等关系
满足的不等关系![]() ,然后得
,然后得![]() ,求得
,求得![]() 的最小值即得结论.
的最小值即得结论.
(1)解![]() ,
,
当![]() 时,
时,![]() 恒成立,函数
恒成立,函数![]() 在
在![]() 上单调递增,无极值.
上单调递增,无极值.
当![]() 时,由
时,由![]() ,得
,得![]() ,函数
,函数![]() 在
在![]() 上单调递增,由
上单调递增,由![]() ,得
,得![]() ,
,
函数![]() 在
在![]() 上单调递减,
上单调递减,![]() 极大值为
极大值为![]() ,无极小值.
,无极小值.
综上所述,当![]() 时,
时,![]() 无极值;
无极值;
当![]() 时,
时,![]() 极大值为
极大值为![]() ,无极小值.
,无极小值.
(2)由![]() 可得
可得![]() ,
,
设![]() ,所以
,所以![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上是增函数,所以
上是增函数,所以![]() 不可能恒成立,
不可能恒成立,
当![]() 时,由
时,由![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递增,当
单调递增,当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
所以当![]() 时,
时,![]() 取最大值,
取最大值,![]() ,
,
所以![]() ,即
,即![]() ,所以
,所以![]() ,
,
令![]() ,
,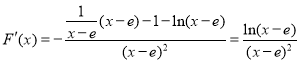 ,
,
当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
所以当![]() 时,
时,![]() 取最小值,即
取最小值,即![]() ,所以
,所以![]() 的最小值为-1.
的最小值为-1.


科目:高中数学 来源: 题型:
【题目】劳动教育是中国特色社会主义教育制度的重要内容,某高中计划组织学生参与各项职业体验,让学生在劳动课程中掌握一定劳动技能,理解劳动创造价值,培养劳动自立意识和主动服务他人、服务社会的情怀.学校计划下周在高一年级开设“缝纫体验课”,聘请“织补匠人”李阿姨给同学们传授织补技艺。高一年级有6个班,李阿姨每周一到周五只有下午第2节课的时间可以给同学们上课,所以必须安排有两个班合班上课,高一年级6个班“缝纫体验课”的不同上课顺序有( )
A.600种B.3600种C.1200种D.1800种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在平行四边形ABCD中,![]() ,
,![]() ,
,![]() ,点E是CD边的中点,将
,点E是CD边的中点,将![]() 沿AE折起,使点D到达点P的位置,且
沿AE折起,使点D到达点P的位置,且![]() .
.

(1)求证;平面![]() 平面ABCE;
平面ABCE;
(2)求点E到平面PAB的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】手机等数码产品中的存储器核心部件是闪存芯片,闪存芯片有两个独立的性能指标:数据传输速度和使用寿命,数据传输速度的单位是![]() ,使用寿命指的是完全擦写的次数(单位:万次).某闪存芯片制造厂为了解产品情况,从一批闪存芯片中随机抽取了100件作为样本进行性能测试,测试数据经过整理得到如下的频率分布直方图(每个分组区间均为左闭右开),其中
,使用寿命指的是完全擦写的次数(单位:万次).某闪存芯片制造厂为了解产品情况,从一批闪存芯片中随机抽取了100件作为样本进行性能测试,测试数据经过整理得到如下的频率分布直方图(每个分组区间均为左闭右开),其中![]() ,
,![]() ,
,![]() 成等差数列且
成等差数列且![]() .
.


(1)估计样本中闪存芯片的数据传输速度的中位数.
(2)估计样本中闪存芯片的使用寿命的平均数.(每组数据以中间值为代表)
(3)规定数据传输速度不低于![]() 为优,使用寿命不低于10万次为优,且两项指标均为优的闪存芯片为
为优,使用寿命不低于10万次为优,且两项指标均为优的闪存芯片为![]() 级产品,仅有一项为优的为
级产品,仅有一项为优的为![]() 级产品,没有优的为
级产品,没有优的为![]() 级产品.现已知样本中有45件
级产品.现已知样本中有45件![]() 级产品,用样本中不同级别产品的频率代替每件产品为相应级别的概率,从这一批产品中任意抽取4件,求其中至少有2件
级产品,用样本中不同级别产品的频率代替每件产品为相应级别的概率,从这一批产品中任意抽取4件,求其中至少有2件![]() 级产品的概率.
级产品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:已知四棱锥P—ABCD的底面ABCD是平行四边形,PA⊥面ABCD,M是AD的中点,N是PC的中点.

(1)求证:MN∥面PAB;
(2)若平面PMC⊥面PAD,求证:CM⊥AD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为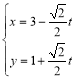 (
(![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的方程为
的方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 与直线
与直线![]() 交于点
交于点![]() ,点
,点![]() 的坐标为(3,1),求
的坐标为(3,1),求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
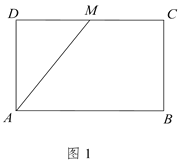
【题目】如图1所示,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 中点,将
中点,将![]() 沿
沿![]() 折起,使点
折起,使点![]() 到点
到点![]() 处,且平面
处,且平面![]() 平面
平面![]() ,如图2所示.
,如图2所示.
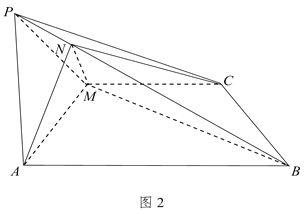
(1)求证:![]() :
:
(2)在棱![]() 上取点
上取点![]() ,使平面
,使平面![]() 平面
平面![]() ,求平面
,求平面![]() 与
与![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 在平面直角坐标系
在平面直角坐标系![]() 下的参数方程为
下的参数方程为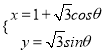 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.
(1)求曲线![]() 的普通方程及极坐标方程;
的普通方程及极坐标方程;
(2)直线![]() 的极坐标方程是
的极坐标方程是![]() ,射线
,射线![]() :
: ![]() 与曲线
与曲线![]() 交于点
交于点![]() 与直线
与直线![]() 交于点
交于点![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com