
【题目】如图,已知平面![]() 平面
平面![]() ,直线
,直线![]() 平面
平面![]() ,且
,且![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() 平面
平面![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)过点![]() 作
作![]() 于点
于点![]() ,推导出
,推导出![]() 平面
平面![]() ,利用线面垂直的性质定理可得出
,利用线面垂直的性质定理可得出![]() ,再由线面平行的判定定理可证得
,再由线面平行的判定定理可证得![]() 平面
平面![]() ;
;
(2)推导出四边形![]() 为矩形,然后以点
为矩形,然后以点![]() 为坐标原点,分别以
为坐标原点,分别以![]() 、
、![]() 、
、![]() 所在直线为
所在直线为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系,设
轴建立空间直角坐标系,设![]() ,利用空间向量法可求得二面角
,利用空间向量法可求得二面角![]() 的余弦值.
的余弦值.
(1)证明:过点![]() 作
作![]() 于点
于点![]() ,
,
因为平面![]() 平面
平面![]() ,又平面
,又平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ;
;
(2)因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
由![]() 可知
可知![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,
所以点![]() 是
是![]() 的中点,连接
的中点,连接![]() ,则
,则![]() ,
,
所以![]() 平面
平面![]() ,则
,则![]() ,
,![]() ,所以四边形
,所以四边形![]() 是矩形.
是矩形.
以![]() 为坐标原点,分别以
为坐标原点,分别以![]() 、
、![]() 、
、![]() 所在直线为
所在直线为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
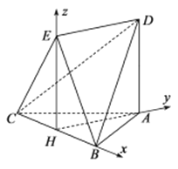
设![]() ,则
,则![]() 、
、![]() 、
、![]() 、
、![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
又![]() ,
,![]() .
.
由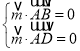 ,得
,得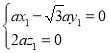 ,取
,取![]() ,得
,得![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
因为![]() ,
,![]() .
.
由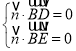 ,得
,得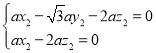 ,取
,取![]() ,得
,得![]() ;
;
设二面角![]() 的平面角为
的平面角为![]() ,则
,则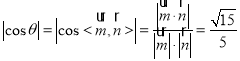 ,
,
由题知二面角![]() 是钝角,则二面角
是钝角,则二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,若△
,若△![]() 的三个顶点都在抛物线
的三个顶点都在抛物线![]() 上,且
上,且![]() ,则称该三角形为“核心三角形”.
,则称该三角形为“核心三角形”.
(1)是否存在“核心三角形”,其中两个顶点的坐标分别为![]() 和
和![]() ?请说明理由;
?请说明理由;
(2)设“核心三角形”![]() 的一边
的一边![]() 所在直线的斜率为4,求直线
所在直线的斜率为4,求直线![]() 的方程;
的方程;
(3)已知△![]() 是“核心三角形”,证明:点
是“核心三角形”,证明:点![]() 的横坐标小于2.
的横坐标小于2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的参数方程;
的参数方程;
(2)若![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司为客户定制了5个险种:甲,一年期短险;乙,两全保险;丙,理财类保险;丁,定期寿险:戊,重大疾病保险,各种保险按相关约定进行参保与理赔.该保险公司对5个险种参保客户进行抽样调查,得出如下的统计图例,以下四个选项错误的是( )



A.54周岁以上参保人数最少B.18~29周岁人群参保总费用最少
C.丁险种更受参保人青睐D.30周岁以上的人群约占参保人群的80%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】CPI是居民消费价格指数(comsummer priceindex)的简称.居民消费价格指数是一个反映居民家庭一般所购买的消费品价格水平变动情况的宏观经济指标.如图是根据国家统计局发布的2019年4月——2020年4月我国CPI涨跌幅数据绘制的折线图(注:2019年6月与2018年6月相比较,叫同比;2019年6月与2019年5月相比较,叫环比),根据该折线图,则下列结论正确的是( )
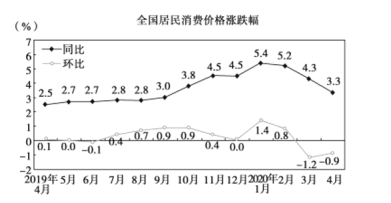
A.2019年4月至2020年4月各月与去年同期比较,CPI有涨有跌
B.2019年4月居民消费价格同比涨幅最小,2020年1月同比涨幅最大
C.2020年1月至2020年4月CPI只跌不涨
D.2019年4月至2019年6月CPI涨跌波动不大,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】冠状病毒是一个大型病毒家族,己知可引起感冒以及中东呼吸综合征(MERS)和严重急性呼吸综合征(SARS)等较严重疾病.而今年出现的新型冠状病毒(nCoV)是以前从未在人体中发现的冠状病毒新毒株.人感染了新型冠状病毒后常见体征有呼吸道症状、发热、咳嗽、气促和呼吸困难等.在较严重病例中,感染可导致肺炎、严重急性呼吸综合征、肾衰竭,甚至死亡.某医院为筛查冠状病毒,需要检验血液是否为阳性,现有![]() 份需检验血液.
份需检验血液.
(1)假设这![]() 份需检验血液有且只有一份为阳性,从中依次不放回的抽取
份需检验血液有且只有一份为阳性,从中依次不放回的抽取![]() 份血液,已知前两次的血液均为阴性,求第
份血液,已知前两次的血液均为阴性,求第![]() 次出现阳性血液的概率;
次出现阳性血液的概率;
(2)现在对![]() 份血液进行检验,假设每份血液的检验结果是阳性还是阴性都是独立的,据统计每份血液是阳性结果的概率为
份血液进行检验,假设每份血液的检验结果是阳性还是阴性都是独立的,据统计每份血液是阳性结果的概率为![]() ,现在有以下两种检验方式:方式一:逐份检验;方式二:混合检验,将
,现在有以下两种检验方式:方式一:逐份检验;方式二:混合检验,将![]() 份血液分别取样混合在一起检验(假设血液混合后不影响血液的检验).若检验结果为阴性,则这
份血液分别取样混合在一起检验(假设血液混合后不影响血液的检验).若检验结果为阴性,则这![]() 份血液全为阴性,检验结束;如果检验结果为阳性,则这
份血液全为阴性,检验结束;如果检验结果为阳性,则这![]() 份血液中有为阳性的血液,为了明确这
份血液中有为阳性的血液,为了明确这![]() 份血液究竟哪几份为阳性,就要对这
份血液究竟哪几份为阳性,就要对这![]() 份再逐份检验.从检验的次数分析,哪一种检验方式更好一些,并说明理由.参考数据:
份再逐份检验.从检验的次数分析,哪一种检验方式更好一些,并说明理由.参考数据:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com