
【题目】已知函数f(x)=aex﹣x,
(1)求f(x)的单调区间,
(2)若关于x不等式aex≥x+b对任意![]() 和正数b恒成立,求
和正数b恒成立,求![]() 的最小值.
的最小值.
【答案】(1)答案见解析.(2)![]()
【解析】
(1)先求导,再分类讨论,根据导数和函数单调性的关系即可求出;
(2)先根据(1)利用导数和函数最值的关系求出![]() ,可得
,可得![]() ,设
,设![]() ,利用导数求出函数的最小值即可.
,利用导数求出函数的最小值即可.
(1)f′(x)=aex﹣1,
当a≤0时,![]() <0,f(x)在R上单调递减,
<0,f(x)在R上单调递减,
若a>0时,令![]() =aex﹣1=0,x=﹣lna,
=aex﹣1=0,x=﹣lna,
在x>﹣lna时,![]() >0,f(x)为增函数,
>0,f(x)为增函数,
在x<﹣lna时,![]() <0,f(x)为减函数,
<0,f(x)为减函数,
所以,当![]() 时,
时,![]() 的单调减区间为
的单调减区间为![]() ,无增区间;
,无增区间;
当![]() 时,
时,![]() 的单调减区间为
的单调减区间为![]() ,增区间为
,增区间为![]() .
.
(2)f(x)=aex﹣x,由题意f(x)min≥b,
由(1)可知,当a≤0时,f(x)在R上单调递减,无最小值,不符合题意,
当a>0时,f(x)min=f(﹣lna)=1+lna≥b,
∴![]() ,
,
设h(a)![]() ,则
,则![]()
![]() ,
,
a∈(0,1],![]() <0;a∈[1,+∞),
<0;a∈[1,+∞),![]() ≥0,
≥0,
∴h(a)min=h(1)=1.
所以![]() 的最小值为
的最小值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】![]() 年
年![]() 月
月![]() 日,某地援鄂医护人员
日,某地援鄂医护人员![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 人(其中
人(其中![]() 是队长)圆满完成抗击新冠肺炎疫情任务返回本地,他们受到当地群众与领导的热烈欢迎.当地媒体为了宣传他们的优秀事迹,让这
是队长)圆满完成抗击新冠肺炎疫情任务返回本地,他们受到当地群众与领导的热烈欢迎.当地媒体为了宣传他们的优秀事迹,让这![]() 名医护人员和接见他们的一位领导共
名医护人员和接见他们的一位领导共![]() 人站一排进行拍照,则领导和队长站在两端且
人站一排进行拍照,则领导和队长站在两端且![]() 相邻,而
相邻,而![]() 不相邻的排法种数为( )
不相邻的排法种数为( )
A.![]() 种B.
种B.![]() 种C.
种C.![]() 种D.
种D.![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高速公路全程设有2n(n≥4,![]() )个服务区.为加强驾驶人员的安全意识,现规划在每个服务区的入口处设置醒目的宣传标语A或宣传标语B.
)个服务区.为加强驾驶人员的安全意识,现规划在每个服务区的入口处设置醒目的宣传标语A或宣传标语B.
(1)若每个服务区入口处设置宣传标语A的概率为![]() ,入口处设置宣传标语B的服务区有X个,求X的数学期望;
,入口处设置宣传标语B的服务区有X个,求X的数学期望;
(2)试探究全程两种宣传标语的设置比例,使得长途司机在走该高速全程中,随机选取3个服务区休息,看到相同宣传标语的概率最小,并求出其最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),以原点
为参数),以原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴建立极坐标系,曲线
轴非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设点![]() ,
,![]() 分别是曲线
分别是曲线![]() ,
,![]() 上两动点且
上两动点且![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过抛物线
经过抛物线![]() 的焦点
的焦点![]() ,
,![]() 上的点
上的点![]() 与
与![]() 的两个焦点所构成的三角形的周长为
的两个焦点所构成的三角形的周长为![]() .
.
(1)求![]() 的方程;
的方程;
(2)若点![]() 关于原点
关于原点![]() 的对称点为
的对称点为![]() ,过点
,过点![]() 作直线
作直线![]() 交
交![]() 于另一点
于另一点![]() ,交
,交![]() 轴于点
轴于点![]() ,且
,且![]() ∥
∥![]() .判断
.判断![]() 是否为定值,若是求出该值;若不是请说明理由.
是否为定值,若是求出该值;若不是请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设关于某设备的使用年限x和所支出的维修费用 y(万元),有如下的统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料可知y对x呈线性相关关系,且线性回归方程为y=a+bx,其中已知b=1.23,请估计使用年限为20年时,维修费用约为_________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,P是椭圆的上顶点,过点P作斜率为
,P是椭圆的上顶点,过点P作斜率为![]() 的直线l交椭圆于另一点A,设点A关于原点的对称点为B
的直线l交椭圆于另一点A,设点A关于原点的对称点为B
(1)求![]() 面积的最大值;
面积的最大值;
(2)设线段PB的中垂线与y轴交于点N,若点N在椭圆内部,求斜率k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知函数![]() 的图象与y轴交于点
的图象与y轴交于点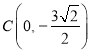 ,与x轴交于A,B两点,其中
,与x轴交于A,B两点,其中![]() ,
,![]() .
.

(1)求函数![]() 的解析式;
的解析式;
(2)将函数![]() 图象上所有点的横坐标缩短为原来的
图象上所有点的横坐标缩短为原来的![]() (纵坐标不变),得到函数
(纵坐标不变),得到函数![]() 的图象,求函数
的图象,求函数![]() 的单调递减区间.
的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,已知等边![]() 的边长为3,点
的边长为3,点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的点,且
上的点,且![]() ,
,![]() .如图2,将
.如图2,将![]() 沿
沿![]() 折起到
折起到![]() 的位置.
的位置.
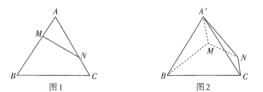
(1)求证:平面![]() 平面
平面![]() ;
;
(2)给出三个条件:①![]() ;②二面角
;②二面角![]() 大小为
大小为![]() ;③
;③![]() .在这三个条件中任选一个,补充在下面问题的条件中,并作答:在线段
.在这三个条件中任选一个,补充在下面问题的条件中,并作答:在线段![]() 上是否存在一点
上是否存在一点![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出
,若存在,求出![]() 的长;若不存在,请说明理由.注:如果多个条件分别解答,按第一个解答给分
的长;若不存在,请说明理由.注:如果多个条件分别解答,按第一个解答给分
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com