
【题目】设数列![]() 满足
满足![]() ,
,![]() 为
为![]() 的前
的前![]() 项和.证明:对任意
项和.证明:对任意![]() ,
,
(1)当![]() 时,
时,![]() ;
;
(2)当![]() 时,
时,![]() ;
;
(3)当![]() 时,
时,![]() .
.
【答案】(1)详见解析;(2)详见解析;(3)详见解析.
【解析】试题解析:
(1)①当![]() 时,显然成立;
时,显然成立;
②假设当![]() ,
,![]() ,
,
则当![]() 时,
时,![]() .
.
由①②,![]() .
.
(2)从而![]() ,
,
即![]() ,
,
于是![]() ,即
,即![]() ;
;
(3)当![]() 时,由(Ⅰ),
时,由(Ⅰ),![]() ,故
,故![]() .
.
令![]() ,由(1)(2),
,由(1)(2),![]() .
.
由![]() ,可得
,可得![]() .
.
从而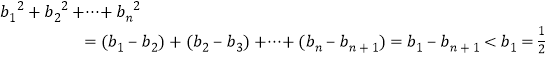 ,
,
又![]() ,
,
故![]() ,即
,即![]() .
.
注意到![]() ,
,
故![]() ,
,
即![]() ,亦即
,亦即![]() .
.
所以当![]() 时,
时,![]() .
.
点睛:本题以数列的通项公式、前![]() 项和有关知识为背景,旨在考查与数列有关的不等式的推理论证能力、分析问题解答问题的能力。解答时,分别采用了分析法、综合法、数学归纳法、放缩法等常用的数学思想方法进行分析推证。不等式的证明问题是高考和各级各类考试的难点内容和题型,求解时应具体问题具体分析灵活采用不同的方法进行综合运用,以达证明之目的。如第一问用的数学归纳法,第二问则是采用的分析缩放的思想进行推证的,第三问则利用数列的递推关系,巧妙地运用缩放的办法进行推证的。
项和有关知识为背景,旨在考查与数列有关的不等式的推理论证能力、分析问题解答问题的能力。解答时,分别采用了分析法、综合法、数学归纳法、放缩法等常用的数学思想方法进行分析推证。不等式的证明问题是高考和各级各类考试的难点内容和题型,求解时应具体问题具体分析灵活采用不同的方法进行综合运用,以达证明之目的。如第一问用的数学归纳法,第二问则是采用的分析缩放的思想进行推证的,第三问则利用数列的递推关系,巧妙地运用缩放的办法进行推证的。


科目:高中数学 来源: 题型:
【题目】某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足函数: 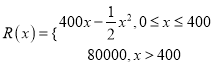 ,其中
,其中![]() 是仪器的月产量
是仪器的月产量
(1)将利润![]() 表示为月产量
表示为月产量![]() 的函数
的函数
(2)当月产量![]() 为何值时,公司所获利润最大?最大利润是多少元?(总收益=总成本+利润)
为何值时,公司所获利润最大?最大利润是多少元?(总收益=总成本+利润)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大家知道, 莫言是中国首位获得诺贝尔奖的文学家, 国人欢欣鼓舞.某高校文学社从男女生中各抽取![]() 名同学调查对莫言作品的了解程度, 结果如下:
名同学调查对莫言作品的了解程度, 结果如下:
阅读过莫言的作品数( 篇) |
|
|
|
|
|
男生 |
|
|
|
|
|
女生 |
|
|
|
|
|
(1)试估计该校学生阅读莫言作品超过![]() 篇的概率;
篇的概率;
(2)对莫言作品阅读超过![]() 篇的则称为“对莫言作品非常了解” , 否则为“ 一般了解” .根据题意完成下表, 并判断能否在犯错误的概率不超过
篇的则称为“对莫言作品非常了解” , 否则为“ 一般了解” .根据题意完成下表, 并判断能否在犯错误的概率不超过![]() 的前提下, 认为对莫言作品非常了解与性别有关?
的前提下, 认为对莫言作品非常了解与性别有关?
非常了解 | 一般了解 | 合计 | |
男生 | |||
女生 | |||
合计 |
附: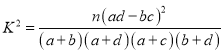 ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列三个集合:
①{x|y=x2+1};
②{y|y=x2+1};
③{(x,y)|y=x2+1}.
(1)它们是不是相同的集合?
(2)它们各自的含义是什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为加快新能源汽车产业发展,推进节能减排,国家鼓励消费者购买新能源汽车,某校研究性学习小组,从汽车市场上随机选取了![]() 辆纯电动乘用车,根据其续驶里程
辆纯电动乘用车,根据其续驶里程![]() (单次充电后能行驶的最大里程)作出了频率与频数的统计表:
(单次充电后能行驶的最大里程)作出了频率与频数的统计表:
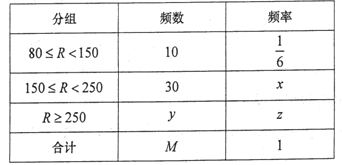
(1)求![]() 的值;
的值;
(2)若用分层抽样的方法从这![]() 辆纯电动乘用车中抽取一个容量为6的样本,从该样本中任选2辆,求选到的2辆车续驶里程为
辆纯电动乘用车中抽取一个容量为6的样本,从该样本中任选2辆,求选到的2辆车续驶里程为![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=a-![]() (a∈R).
(a∈R).
(1) 判断函数f(x)的单调性并给出证明;
(2) 若存在实数a使函数f(x)是奇函数,求a;
(3)对于(2)中的a,若f(x)≥![]() ,当x∈[2,3]时恒成立,求m的最大值.
,当x∈[2,3]时恒成立,求m的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com