练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知点是平行四边形所在平面外一点，如果，，．对于结论：

    ①；②；

    ③是平面的法向量；

    ④．

    其中正确的个数是（    ）

    A．1        B．2        C．3        D．4

     

    【答案】

    C

    【解析】

    试题分析： 因为·=(2，－1，－4)·（－1,2,1）=－2－2＋4=0，所以；

    因为·=(4，2，0)·（－1,2,1）=－4＋4＋0=0，所以；

    因为，，所以是平面的法向量；

    因为=－=(4，2，0)－(2，－1，－4)=(2，3，4)，所以，故正确命题有3个，选D.

    考点：本题主要考查向量的坐标运算、向量的共线与垂直。

    点评：利用共线、垂直的充要条件判断。

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如图，已知四棱锥V-ABCD，底面ABCD是平行四边形，点V在平面ABCD上的射影E在AD边上，且AE=
    1
    3
    ED    ，VE=4，BE=EC=2，∠BEC=90°．
    （Ⅰ）设F是BC的中点，求异面直线EF与VC所成角的余弦值；
    （Ⅱ）设点P在棱VC上，且DP⊥EC．求
    VP
    PC
    的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

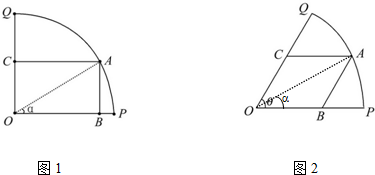    精英家教网如图1所示，已知OPQ是半径为1，圆心角为θ的扇形，A是扇形弧PQ上的动点，AB∥OQ，OP与AB交于点B，AC∥OP，OQ与AC交于点C．记∠AOP=α．
    （1）若θ=
    π
    2
    ，如图1，当角α取何值时，能使矩形ABOC的面积最大；
    （2）若θ=
    π
    3
    ，如图2，当角α取何值时，能使平行四边形ABOC的面积最大．并求出最大面积．

    查看答案和解析>>

    科目：高中数学 来源：2015届浙江绍兴一中高二第一学期期中测试文科数学试卷（解析版） 题型：解答题

    如图，已知四棱锥，底面是平行四边形，点在平面上的射影在边上，且，．

    （Ⅰ）设是的中点，求异面直线与所成角的余弦值；

    （Ⅱ）设点在棱上，且．求的值．

     

    查看答案和解析>>

    科目：高中数学 来源：2013届北京市高二上学期期中考试理科数学 题型：解答题

    （（本题满分14分）已知，如图四棱锥P—ABCD中，底面ABCD是平行四边形，PG⊥平面ABCD，垂足为G，G在AD上，且AG=GD，BG⊥GC，GB=GC=2，E是BC的中点，四面体P—BCG的体积为．（Ⅰ）求异面直线GE与PC所成角的余弦；（Ⅱ）求点D到平面PBG的距离；（Ⅲ）若F点是棱PC上一点，且DF⊥GC，求的值．

     

    查看答案和解析>>

    科目：高中数学 来源：同步题 题型：证明题

    如图所示，已知P 是平行四边形ABCD 所在平面外一点，连结PA 、PB 、PC 、PD ，点E 、F 、G 、H 分别为△PAB 、△PBC 、△PCD 、 △PDA 的重心，求证：E 、F 、G 、H 四点共面

    查看答案和解析>>

    同步练习册答案