
【题目】数列![]() 的前
的前![]() 项1,3,7,
项1,3,7,![]() ,
,![]() (
(![]() )组成集合
)组成集合![]() ,从集合
,从集合![]() 中任取
中任取![]() (
(![]() )个数,其所有可能的
)个数,其所有可能的![]() 个数的乘积的和为
个数的乘积的和为![]() (若只取一个数,规定乘积为此数本身),记
(若只取一个数,规定乘积为此数本身),记![]() .例如:当
.例如:当![]() 时,
时,![]() ,
,![]() ,
,![]() ;
;![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)当![]() 时,求
时,求![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)证明:![]() 时集合
时集合![]() 的
的![]() 与
与![]() 时集合
时集合![]() 的
的![]() (为以示区别,用
(为以示区别,用![]() 表示)有关系式
表示)有关系式![]() (
(![]() ,
,![]() );
);
(3)试求![]() (用
(用![]() 表示).
表示).
【答案】(1)![]() ,
,![]() ,
,![]() ,
,![]() (2)见解析(3)
(2)见解析(3)![]()
【解析】
(1)当![]() 时,得出
时,得出![]() ,根据定义得出
,根据定义得出![]() 、
、![]() 、
、![]() 的值,可计算出
的值,可计算出![]() 的值;
的值;
(2)当![]() 时,集合
时,集合![]() 有
有![]() 个元素,比
个元素,比![]() 时的集合
时的集合![]() 多了一个元素;
多了一个元素;
![]() ,对应的
,对应的![]() 包含两个部分:(i)若
包含两个部分:(i)若![]() 不含
不含![]() ,则
,则![]() 中的任何一项恰好为
中的任何一项恰好为![]() 时集合
时集合![]() 的对应的
的对应的![]() 中的一项;(ii)若
中的一项;(ii)若![]() 中含
中含![]() 的任何一项,除了
的任何一项,除了![]() ,其余的
,其余的![]() 个数均来自集合
个数均来自集合![]() ,这
,这![]() 个数的乘积恰好为集合
个数的乘积恰好为集合![]() 所对应的
所对应的![]() 中的一项,即可证明;
中的一项,即可证明;
(3)由![]() ,
,![]() ,
,![]() ,猜想
,猜想![]() ,下面利用数学归纳法进行即可.
,下面利用数学归纳法进行即可.
(1)当![]() 时,
时,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]()
(2)证明:当![]() 时,集合
时,集合![]() 有
有![]() 个元素,比
个元素,比![]() 时的集合
时的集合![]() 多了一个元素:
多了一个元素:![]() .∴对应的
.∴对应的![]() 包含两个部分:
包含两个部分:
若![]() 中不含
中不含![]() ,则
,则![]() 中的任何一项恰好为
中的任何一项恰好为![]() 时集合
时集合![]() 的对应的
的对应的![]() 中的一项.
中的一项.
若![]() 中含
中含![]() 的任何一项,除了
的任何一项,除了![]() ,其余的
,其余的![]() 个数均来自集合
个数均来自集合![]() ,这
,这![]() 个数的乘积恰好为集合
个数的乘积恰好为集合![]() 所对应的
所对应的![]() 中的一项.
中的一项.
∴有关系式![]()
(3)解:由![]() ,
,![]() ,
,![]() ,
,
猜想![]() .下面证明:(i)易知
.下面证明:(i)易知![]() 时成立.
时成立.
(ii)假设![]() 时,
时,![]() ,
,
则![]() 时,
时,![]()
![]()
(其中![]() ,
,![]() ,2,…,k,为
,2,…,k,为![]() 时可能的k个数的乘积的和为
时可能的k个数的乘积的和为![]() ,
,
![]()
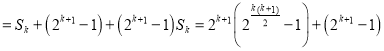
![]() ,即
,即![]() 时,
时,![]() 也成立,
也成立,
综合(i)(ii)知对![]() ,
,![]() 成立.
成立.
∴![]() .
.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
【题目】某地的中小学办学条件在政府的教育督导下,迅速得到改变.教育督导一年后.分别随机抽查了初中(用![]() 表示)与小学(用
表示)与小学(用![]() 表示)各10所学校.得到相关指标的综合评价得分(百分制)的茎叶图如图所示.则从茎叶图可得出正确的信息为( )(80分及以上为优秀). ①初中得分与小学得分的优秀率相同;②初中得分与小学得分的中位数相同③初中得分的方差比小学得分的方差大④初中得分与小学得分的平均分相同.
表示)各10所学校.得到相关指标的综合评价得分(百分制)的茎叶图如图所示.则从茎叶图可得出正确的信息为( )(80分及以上为优秀). ①初中得分与小学得分的优秀率相同;②初中得分与小学得分的中位数相同③初中得分的方差比小学得分的方差大④初中得分与小学得分的平均分相同.

A.①②B.①③C.②④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国铁路总公司相关负责人表示,到2018年底,全国铁路营业里程达到13.1万公里,其中高铁营业里程2.9万公里,超过世界高铁总里程的三分之二,下图是2014年到2018年铁路和高铁运营里程(单位:万公里)的折线图,以下结论不正确的是( )

A.每相邻两年相比较,2014年到2015年铁路运营里程增加最显著
B.从2014年到2018年这5年,高铁运营里程与年价正相关
C.2018年高铁运营里程比2014年高铁运营里程增长80%以上
D.从2014年到2018年这5年,高铁运营里程数依次成等差数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在平面四边形![]() 中,
中,![]() ,现将
,现将![]() 沿四边形
沿四边形![]() 的对角线
的对角线![]() 折起,使点
折起,使点![]() 运动到点
运动到点![]() ,如图2,这时平面
,如图2,这时平面![]() 平面
平面![]() .
.
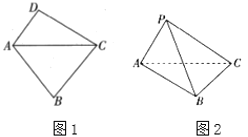
(1)求直线![]() 与平面
与平面![]() 所成角的正切值;
所成角的正切值;
(2)求二面角![]() 的正切值.
的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂因排污比较严重,决定着手整治,一个月时污染度为![]() ,整治后前四个月的污染度如下表:
,整治后前四个月的污染度如下表:
月数 |
|
|
|
| … |
污染度 |
|
|
|
| … |
污染度为![]() 后,该工厂即停止整治,污染度又开始上升,现用下列三个函数模拟从整治后第一个月开始工厂的污染模式:
后,该工厂即停止整治,污染度又开始上升,现用下列三个函数模拟从整治后第一个月开始工厂的污染模式:![]() ,
,![]() ,
,![]() ,其中
,其中![]() 表示月数,
表示月数,![]() 、
、![]() 、
、![]() 分别表示污染度.
分别表示污染度.
(1)问选用哪个函数模拟比较合理,并说明理由;
(2)若以比较合理的模拟函数预测,整治后有多少个月的污染度不超过![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥![]() 中,
中,![]() 底面
底面![]() 为等边三角形,
为等边三角形,![]() 分别是
分别是![]() 的中点.
的中点.
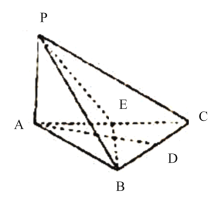
(1)证明:平面![]() 平面
平面![]() ;
;
(2)如何在![]() 上找一点
上找一点![]() ,使
,使![]() 平面
平面![]() 并说明理由;
并说明理由;
(3)若![]() ,对于(2)中的点
,对于(2)中的点![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,且点
,且点![]() 在椭圆C上.
在椭圆C上.
(1)求椭圆C的标准方程;
(2)过椭圆 上异于其顶点的任意一点Q作圆
上异于其顶点的任意一点Q作圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() 不在坐标轴上),若直线
不在坐标轴上),若直线![]() 在x轴,y轴上的截距分别为
在x轴,y轴上的截距分别为![]() ,证明:
,证明:![]() 为定值;
为定值;
(3)若![]() 是椭圆
是椭圆![]() 上不同两点,
上不同两点,![]() 轴,圆E过
轴,圆E过![]() ,且椭圆
,且椭圆![]() 上任意一点都不在圆E内,则称圆E为该椭圆的一个内切圆,试问:椭圆
上任意一点都不在圆E内,则称圆E为该椭圆的一个内切圆,试问:椭圆![]() 是否存在过焦点F的内切圆?若存在,求出圆心E的坐标;若不存在,请说明理由.
是否存在过焦点F的内切圆?若存在,求出圆心E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了应对金融危机,决定适当进行裁员,已知这家公司现有职工![]() 人(
人(![]() ,且
,且![]() 为10的整数倍),每人每年可创利100千元,据测算,在经营条件不变的前的提下,若裁员人数不超过现有人数的30%,则每裁员1人,留岗员工每人每年就能多创利1千元(即若裁员
为10的整数倍),每人每年可创利100千元,据测算,在经营条件不变的前的提下,若裁员人数不超过现有人数的30%,则每裁员1人,留岗员工每人每年就能多创利1千元(即若裁员![]() 人,留岗员工可多创利润
人,留岗员工可多创利润![]() 千元);若裁员人数超过现有人数的30%,则每裁员1人,留岗员工每人每年就能多创利2千元(即若裁员
千元);若裁员人数超过现有人数的30%,则每裁员1人,留岗员工每人每年就能多创利2千元(即若裁员![]() 人,留岗员工可多创利润
人,留岗员工可多创利润![]() 千元),为保证公司的正常运转,留岗的员工数不得少于现有员工人数的50%,为了保障被裁员工的生活,公司要付给被裁员工每人每年20千元的生活费.
千元),为保证公司的正常运转,留岗的员工数不得少于现有员工人数的50%,为了保障被裁员工的生活,公司要付给被裁员工每人每年20千元的生活费.
(1)设公司裁员人数为![]() ,写出公司获得的经济效益
,写出公司获得的经济效益![]() (千元)关于
(千元)关于![]() 的函数(经济效益=在职人员创利总额—被裁员工生活费);
的函数(经济效益=在职人员创利总额—被裁员工生活费);
(2)为了获得最大的经济效益,该公司应裁员多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 为两非零有理数列(即对任意的
为两非零有理数列(即对任意的![]() ,
,![]() 均为有理数),
均为有理数),![]() 为一无理数列(即对任意的
为一无理数列(即对任意的![]() ,
,![]() 为无理数).
为无理数).
(1)已知![]() ,并且
,并且![]() 对任意的
对任意的![]() 恒成立,试求
恒成立,试求![]() 的通项公式.
的通项公式.
(2)若![]() 为有理数列,试证明:对任意的
为有理数列,试证明:对任意的![]() ,
,![]() 恒成立的充要条件为
恒成立的充要条件为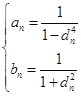 .
.
(3)已知![]() ,
,![]() ,对任意的
,对任意的![]() ,
,![]() 恒成立,试计算
恒成立,试计算![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com