练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数且.

    （1）若函数区间上单调递增，求实数的取值范围；

    （2）设函数， 为自然对数的底数.若存在，使不等式成立，求实数的取值范围.

    【答案】（1）；（2）.

    【解析】试题分析：（1）函数单调递增转化为导数恒为正值，分类讨论求即可；（2）分离参数，转化为求函数的最值，利用导数即可求出最值。

    试题解析：（1）当时，函数是上的单调递增函数，符合题意；

    当时，由，得，

    ∵函数在区间内单调递增，

    ∴，则.

    综上所述，实数的取值范围是.

    （另由对恒成立可得，当时，符合；

    当时， ，即，∴.

    综上）

    （2）∵存在，使不等式成立，

    ∴存在，使成立.

    令，从而，

    .

    由（1）知当时， 在上递增，∴.

    ∴在上恒成立.

    ∴，

    ∴在上单调递增.

    ∴，∴.

    实数的取值范围为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】椭圆 =1上有一点M（﹣4， ）在抛物线y2=2px（p＞0）的准线l上，抛物线的焦点也是椭圆焦点．
    （1）求椭圆的标准方程；
    （2）若点N在抛物线上，过N作准线l的垂线，垂足为Q，求|MN|+|NQ|的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）=emx+x2﹣mx．
    （1）证明：f（x）在（﹣∞，0）单调递减，在（0，+∞）单调递增；
    （2）若对于任意x1 ， x2∈[﹣1，1]，都有|f（x1）﹣f（x2）|≤e﹣1，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数是的一个极值点.

    （1）若是的唯一极值点，求实数的取值范围；

    （2）讨论的单调性；

    （3）若存在正数，使得，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数y= 的定义域是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）=1﹣ （x∈R），
    （1）求反函数f﹣1（x）；
    （2）解不等式f﹣1（x）＞log2（1+x）+1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数

    （1）当， 恒成立，求实数的取值范围.

    （2）设在上有两个极值点.

    （A）求实数的取值范围；

    （B）求证： .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知a＞0，集合A={x|ax2﹣2x+2a﹣1=0}，B={y|y=log2（x+ ﹣4）}，p：A=，q：B=R．
    （1）若p∧q为真，求a的最大值；
    （2）若p∧q为为假，p∨q为真，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知具有相关关系的两个变量之间的几组数据如下表所示：

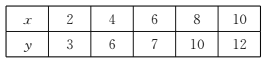
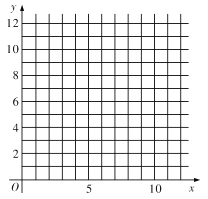
    （1）请根据上表数据在网格纸中绘制散点图；

    （2）请根据上表提供的数据，用最小二乘法求出关于的线性回归方程，并估计当时， 的值；

    （3）将表格中的数据看作五个点的坐标，从这五个点中随机抽取2个点，求这两个点都在直线的右下方的概率.

    （参考公式： ， ）

    查看答案和解析>>

    同步练习册答案