练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    函数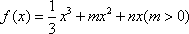在x＝1处取得极值，(x)的最小值为－4．

    (1)求m，n的值及f(x)的单调区间；

    (2)试分别求方程f(x)－c＝0在区间[－4，1]上有一根、有两根时c的范围．

    答案：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：北京市崇文区2006－2007学年度高三年级第一学期期末统一考试、数学文 题型：013

    已知f(x)的定义域为R，f(x)的导函数f′(x)的图象如所示，则

    [　　]

    A．f(x)在x＝1处取得极小值

    B．f(x)在x＝1处取得极大值

    C．f(x)是R上的增函数

    D．f(x)是(－∞，1)上的减函数，(1，＋∞)上的增函数

    查看答案和解析>>

    科目：高中数学 来源：学习周报　数学　北师大课标高二版(选修2－2)　2009－2010学年　第35期　总第191期 北师大课标 题型：013

    函数y＝2x3－3x2

    [　　]
    A．

    在x＝0处取得极大值0，但无极小值

    B．

    在x＝1处取得极小值－1，但无极大值

    C．

    在x＝0处取得极大值0，在x＝1处取得极小值－1

    D．

    以上都不对

    查看答案和解析>>

    科目：高中数学 来源：江西省重点中学协作体2012届高三第一次联考数学理科试题 题型：044

    已知函数f(x)＝(ax2＋bx＋c)ex在x＝1处取得极小值，其图象过点A(0，1)，且在点A处切线的斜率为－1．

    (Ⅰ)求f(x)的解析式；

    (Ⅱ)设函数g(x)的定义域D，若存在区间[m，n]D，使得g(x)在[m，n]上的值域也是[m，n]，则称区间[m，n]为函数g(x)的“保值区间”．证明：当x＞1时，函数f(x)不存在“保值区间”；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知f(x)的定义域为R，f(x)的导函数f′(x)的图像如图所示，则        (　　)                                                                                        (　　)

    A．f(x)在x＝1处取得极小值

    B．f(x)在x＝1处取得极大值

    C．f(x)在R上的增函数

    D．f(x)在(－∞，1)上是减函数，(1，＋∞)上是增函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    函数y＝2x3-3x2


    1. A.
      在x＝0处取得极大值0，但无极小值
    2. B.
      在x＝1处取得极小值-1，但无极大值
    3. C.
      在x＝0处取得极大值0，在x＝1处取得极小值-1
    4. D.
      以上都不对

    查看答案和解析>>

    同步练习册答案