
| 2 | 75 |
| k |
| x |
| 500 | ||
|
| x |
| 2 |
| 75 |
| 250 | ||
|
| 6 |
| 75 |
| 250 | ||
|
| 6 |
| 75 |


科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
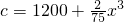 (单位:万元);该饰品单价p(单位:元)的平方与生产的饰品件数x(单位:万件)成反比,现已知生产该饰品100万件时,其单价p=50元.且工厂生产的饰品都可以销售完.设工厂生产该饰品的利润为f(x)(万元)(注:利润=销售额-成本)
(单位:万元);该饰品单价p(单位:元)的平方与生产的饰品件数x(单位:万件)成反比,现已知生产该饰品100万件时,其单价p=50元.且工厂生产的饰品都可以销售完.设工厂生产该饰品的利润为f(x)(万元)(注:利润=销售额-成本)查看答案和解析>>
科目:高中数学 来源: 题型:
某商家经亚组委授权销售广州亚运吉祥物“乐羊羊”小饰品,该饰品的成本是5元/件,开始按8元/件销售,日销售量为50件,为了获取最大利润,商家先后采取了提价与降价两种措施进行试销。经试销发现:销售价每上涨1元,每天销售量就减少10件;而降价后,日销售量Q(件)与实际销售价x(元)满足关系:
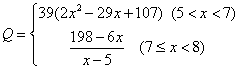
(Ⅰ)求商家经销该饰品每天的总利润y(元)与实际销售价x(元)的函数关系式;
(注:利润=销售额-成本)
(Ⅱ)试问:当实际销售价为多少元时,商家每天的总利润最大.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖北省孝感高级中学高二(下)期中数学试卷(文科)(解析版) 题型:解答题
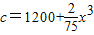 (单位:万元);该饰品单价p(单位:元)的平方与生产的饰品件数x(单位:万件)成反比,现已知生产该饰品100万件时,其单价p=50元.且工厂生产的饰品都可以销售完.设工厂生产该饰品的利润为f(x)(万元)(注:利润=销售额-成本)
(单位:万元);该饰品单价p(单位:元)的平方与生产的饰品件数x(单位:万件)成反比,现已知生产该饰品100万件时,其单价p=50元.且工厂生产的饰品都可以销售完.设工厂生产该饰品的利润为f(x)(万元)(注:利润=销售额-成本)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com