
【题目】如图,在一条景观道的一端有一个半径为![]() 米的圆形摩天轮O,逆时针
米的圆形摩天轮O,逆时针![]() 分钟转一圈,从
分钟转一圈,从![]() 处进入摩天轮的座舱,
处进入摩天轮的座舱,![]() 垂直于地面
垂直于地面![]() ,在距离
,在距离![]() 处
处![]() 米处设置了一个望远镜
米处设置了一个望远镜![]() .
.

(1)同学甲打算独自乘坐摩天轮,但是其母亲不放心,于是约定在登上摩天轮座舱![]() 分钟后,在座舱内向其母亲挥手致意,而其母亲则在望远镜
分钟后,在座舱内向其母亲挥手致意,而其母亲则在望远镜![]() 中仔细观看.问望远镜
中仔细观看.问望远镜![]() 的仰角
的仰角![]() 应调整为多少度?(精确到1度)
应调整为多少度?(精确到1度)
(2)在同学甲向其母亲挥手致意的同时,同一座舱的另一名乘客乙在拍摄地面上的一条绿化带![]() ,发现取景的视角
,发现取景的视角![]() 恰为
恰为![]() ,求绿化带
,求绿化带![]() 的长度(精确到1米)
的长度(精确到1米)
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】日照一中为了落实“阳光运动一小时”活动,计划在一块直角三角形ABC的空地上修建一个占地面积为S的矩形AMPN健身场地.如图,点M在AC上,点N在AB上,且P点在斜边BC上,已知∠ACB=60°且|AC|=30米,|AM|=x米,x∈[10,20].
(1)试用x表示S,并求S的取值范围;
(2)若在矩形AMPN以外(阴影部分)铺上草坪.已知:矩形AMPN健身场地每平方米的造价为![]() ,草坪的每平方米的造价为
,草坪的每平方米的造价为![]() (k为正常数).设总造价T关于S的函数为T=f(S),试问:如何选取|AM|的长,才能使总造价T最低.
(k为正常数).设总造价T关于S的函数为T=f(S),试问:如何选取|AM|的长,才能使总造价T最低.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有10个不同的产品,其中4个次品,6个正品.现每次取其中一个进行测试,直到4个次品全测完为止,若最后一个次品恰好在第五次测试时被发现,则该情况出现的概率是_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一块平行四边形绿地![]() ,经测量
,经测量![]() 百米,
百米,![]() 百米,
百米,![]() ,拟过线段
,拟过线段![]() 上一点
上一点![]() 设计一条直路
设计一条直路![]() (点
(点![]() 在四边形
在四边形![]() 的边上,不计路的宽度),
的边上,不计路的宽度),![]() 将绿地分成两部分,且右边面积是左边面积的3倍,设
将绿地分成两部分,且右边面积是左边面积的3倍,设![]() 百米,
百米,![]() 百米.
百米.
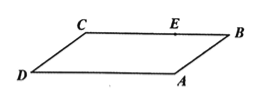
(1)当点![]() 与点
与点![]() 重合时,试确定点
重合时,试确定点![]() 的位置;
的位置;
(2)试求![]() 的值,使路
的值,使路![]() 的长度
的长度![]() 最短.
最短.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() 满足
满足![]() .
.
①存在![]() 可以生成的数列
可以生成的数列![]() 是常数数列;
是常数数列;
②“数列![]() 中存在某一项
中存在某一项![]() ”是“数列
”是“数列![]() 为有穷数列”的充要条件;
为有穷数列”的充要条件;
③若![]() 为单调递增数列,则
为单调递增数列,则![]() 的取值范围是
的取值范围是![]() ;
;
④只要![]() ,其中
,其中![]() ,则
,则![]() 一定存在;
一定存在;
其中正确命题的序号为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我市为改善空气环境质量,控制大气污染,政府相应出台了多项改善环境的措施.其中一项是为了减少燃油汽车对大气环境污染.从2018年起大力推广使用新能源汽车,鼓励市民如果需要购车,可优先考虑选用新能源汽车.政府对购买使用新能源汽车进行购物补贴,同时为了地方经济发展,对购买本市企业生产的新能源汽车比购买外地企业生产的新能源汽车补贴高.所以市民对购买使用本市企业生产的新能源汽车的满意度也相应有所提高.有关部门随机抽取本市本年度内购买新能源汽车的![]() 户,其中有
户,其中有![]() 户购买使用本市企业生产的新能源汽车,对购买使用新能源汽车的满意度进行调研,满意度以打分的形式进行.满分
户购买使用本市企业生产的新能源汽车,对购买使用新能源汽车的满意度进行调研,满意度以打分的形式进行.满分![]() 分,将分数按照
分,将分数按照![]() 分成5组,得如下频率分布直方图.
分成5组,得如下频率分布直方图.

(1)若本次随机抽取的样本数据中购买使用本市企业生产的新能源汽车的用户中有![]() 户满意度得分不少于
户满意度得分不少于![]() 分,把得分不少于
分,把得分不少于![]() 分为满意.根据提供的条件数据,完成下面的列联表.
分为满意.根据提供的条件数据,完成下面的列联表.
满意 | 不满意 | 总计 | |
购本市企业生产的新能源汽车户数 | |||
购外地企业生产的新能源汽车户数 | |||
总计 |
并判断是否有![]() 的把握认为购买使用新能源汽车的满意度与产地有关?
的把握认为购买使用新能源汽车的满意度与产地有关?
(2)以频率作为概率,政府对购买使用新能源汽车的补贴标准是:购买本市企业生产的每台补贴![]() 万元,购买外地企业生产的每台补贴
万元,购买外地企业生产的每台补贴![]() 万元.但本市本年度所有购买新能源汽车的补贴每台的期望值不超过
万元.但本市本年度所有购买新能源汽车的补贴每台的期望值不超过![]() 万元.则购买外地产的新能源汽车每台最多补贴多少万元?
万元.则购买外地产的新能源汽车每台最多补贴多少万元?
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项均为正数的数列{an}的前n项和Sn满足S1>1,且![]() (nN*).
(nN*).
(1)求{an}的通项公式;
(2)设数列![]() 满足
满足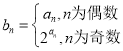 ,Tn为数列{bn}的前n项和,求Tn;
,Tn为数列{bn}的前n项和,求Tn;
(3)设![]() *(
*(![]() 为正整数),问是否存在正整数
为正整数),问是否存在正整数![]() ,使得当任意正整数n>N时恒有Cn>2015成立?若存在,请求出正整数
,使得当任意正整数n>N时恒有Cn>2015成立?若存在,请求出正整数![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com