
【题目】如图,在三棱锥P-ABC中,平面![]() 平面ABC,
平面ABC,![]() ,
,![]() .
.
(1)若![]() ,求证:平面
,求证:平面![]() 平面PBC;
平面PBC;
(2)若PA与平面ABC所成的角为![]() ,求二面角C-PB-A的余弦值.
,求二面角C-PB-A的余弦值.
【答案】(1)见解析 (2)![]()
【解析】
(1)利用面面垂直的性质定理证明![]() 平面
平面![]() ,由此即可证明平面
,由此即可证明平面![]() 平面
平面![]() ;
;
(2)根据条件建立空间直角坐标系,求解出平面![]() 、平面
、平面![]() 的法向量,利用法向量夹角的余弦值求解出二面角
的法向量,利用法向量夹角的余弦值求解出二面角![]() 的余弦值.
的余弦值.
解:(1)证明:因为平面![]() 平面ABC,平面
平面ABC,平面![]() 平面
平面![]() ,
,![]() 平面ABC,
平面ABC,![]() ,
,
所以![]() 平面PAC,由
平面PAC,由![]() 平面PAC,所以
平面PAC,所以![]() ,
,
又因为![]()
![]() ,所以
,所以![]() 平面PBC,
平面PBC,
因为![]() 平面PAB,所以平面
平面PAB,所以平面![]() 平面PBC;
平面PBC;
(2)过P作![]() ,因为平面
,因为平面![]() 平面ABC,
平面ABC,
所以![]() 平面ABC,所以
平面ABC,所以![]() ,
,
不妨设![]() ,所以
,所以![]() ,
,
以C为原点,分别以CA,CB所在的直线为x,y轴,以过C点且平行于PH的直线为z轴,
建立空间直角坐标系如图所示,
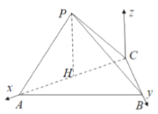
则![]()
![]()
![]()
![]() ,
,
![]()
![]() ,
,![]()
![]() ,
,
设![]() 为面PAB的一个法向量,
为面PAB的一个法向量,
则有![]()
![]() ,即
,即 ,令
,令![]() ,可得
,可得![]() ,
,
设![]() 为面PBC的一个法向量,
为面PBC的一个法向量,
则有![]()
![]() ,即
,即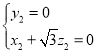 ,令
,令![]() ,可得
,可得![]() ,
,
所以![]()
![]() ,
,
所以二面角C-PB-A的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】条形图给出的是2017年全年及2018年全年全国居民人均可支配收入的平均数与中位数,饼图给出的是2018年全年全国居民人均消费及其构成,现有如下说法:
①2018年全年全国居民人均可支配收入的平均数的增长率低于2017年;
②2018年全年全国居民人均可支配收入的中位数约是平均数的![]() ;
;
③2018年全年全国居民衣(衣着)食(食品烟酒)住(居住)行(交通通信)的支出超过人均消费的![]() .
.
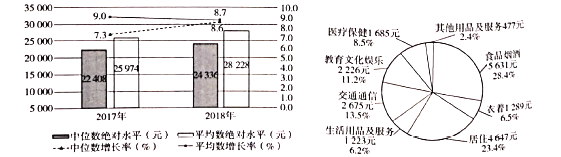
则上述说法中,正确的个数是( )
A. 3B. 2C. 1D. 0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]()
![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() ,过
,过![]() 的直线交椭圆于
的直线交椭圆于![]() ,
,![]() 两点,若椭圆
两点,若椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设不经过椭圆的中心而平行于弦![]() 的直线交椭圆
的直线交椭圆![]() 于点
于点![]() ,
,![]() ,设弦
,设弦![]() ,
,![]() 的中点分别为
的中点分别为![]() ,证明:
,证明:![]() 三点共线.
三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为F,准线为l,过F的直线与E交于A,B两点,C,D分别为A,B在l上的射影,且
的焦点为F,准线为l,过F的直线与E交于A,B两点,C,D分别为A,B在l上的射影,且![]() ,M为AB中点,则下列结论正确的是( )
,M为AB中点,则下列结论正确的是( )
A.![]() B.
B.![]() 为等腰直角三角形
为等腰直角三角形
C.直线AB的斜率为![]() D.
D.![]() 的面积为4
的面积为4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线![]() :
:![]() 过点
过点![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)设![]() 为
为![]() 轴上一点,
轴上一点,![]() 为抛物线上任意一点,求
为抛物线上任意一点,求![]() 的最小值;
的最小值;
(3)过抛物线![]() 的焦点
的焦点![]() ,作相互垂直的两条弦
,作相互垂直的两条弦![]() 和
和![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的四个顶点组成的四边形的面积为
的四个顶点组成的四边形的面积为![]() ,且经过点
,且经过点 .
.

(1)求椭圆![]() 的方程;
的方程;
(2)若椭圆![]() 的下顶点为
的下顶点为![]() ,如图所示,点
,如图所示,点![]() 为直线
为直线![]() 上的一个动点,过椭圆
上的一个动点,过椭圆![]() 的右焦点
的右焦点![]() 的直线
的直线![]() 垂直于
垂直于![]() ,且与
,且与![]() 交于
交于![]() 两点,与
两点,与![]() 交于点
交于点![]() ,四边形
,四边形![]() 和
和![]() 的面积分别为
的面积分别为![]() .求
.求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的六面体中,四边形![]() 是边长为
是边长为![]() 的正方形,四边形
的正方形,四边形![]() 是梯形,
是梯形,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,![]() .
.
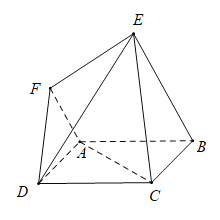
(1)在图中作出平面 ![]() 与平面
与平面![]() 的交线,并写出作图步骤,但不要求证明;
的交线,并写出作图步骤,但不要求证明;
(2)求证:![]() 平面
平面![]() ;
;
(3)求平面![]() 与平面
与平面![]() 所成角的余弦值
所成角的余弦值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com