
 上三点A(x1,y1),B(4,y2),C(x3,y3)和焦点F(4,0)的距离依次成等差数列.
上三点A(x1,y1),B(4,y2),C(x3,y3)和焦点F(4,0)的距离依次成等差数列. -x1|+|
-x1|+| -x3|=2|
-x3|=2| -4|;
-4|; ;
;
 =0,故得
=0,故得 ,即k=-
,即k=- ,故t=-
,故t=-
 ,故垂直平分线方程为y-t=
,故垂直平分线方程为y-t= (x-4)即y+
(x-4)即y+ =
= (x-4)故有y=
(x-4)故有y= (x-4+
(x-4+ )=
)= (x-
(x- )
) (x-
(x- )
)


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
| 3 |
| y2 |
| a2 |
| x2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
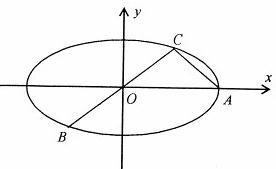 如图:已知椭圆A,B,C是长轴长为4的椭圆上三点,点A是长轴的一个端点,BC过椭圆的中心O,且
如图:已知椭圆A,B,C是长轴长为4的椭圆上三点,点A是长轴的一个端点,BC过椭圆的中心O,且| AC |
| BC |
| BC |
| AC |
| PQ |
| AB |
查看答案和解析>>
科目:高中数学 来源: 题型:
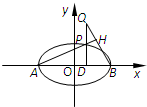 如图,已知椭圆
如图,已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 3 |
| PQ |
| QD |
查看答案和解析>>
科目:高中数学 来源:南通模拟 题型:解答题
| 3 |
| y2 |
| a2 |
| x2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源:2013年全国名校高考数学模拟试卷1(理科)(解析版) 题型:解答题
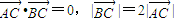 .
.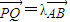 ?请给出证明.
?请给出证明.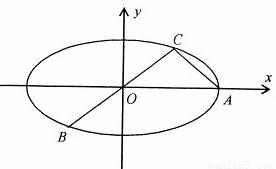
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com