
【题目】(题文)
等边△ABC的边长为3,点D,E分别为AB,AC上的点,且满足![]() (如图①),将△ADE沿DE折起到△A1DE的位置,使二面角A1﹣DE﹣B成直二面角,连接A1B,A1C(如图②).
(如图①),将△ADE沿DE折起到△A1DE的位置,使二面角A1﹣DE﹣B成直二面角,连接A1B,A1C(如图②).
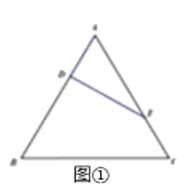
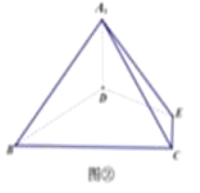
(1)求证:A1D⊥平面BCED;
(2)在线段BC上是否存在点P(不包括端点),使直线PA1与平面A1BD所成的角为60°?若存在,求出A1P的长,若不存在,请说明理由.
【答案】(1)证明见解析(2)存在;A1P![]()
【解析】
(1)计算![]() ,利用勾股定理可证A1D⊥DE,再根据面面垂直的性质得出
,利用勾股定理可证A1D⊥DE,再根据面面垂直的性质得出![]() 平面
平面![]() ;
;
(2)建立空间坐标系,设![]() ,求出平面
,求出平面![]() 的法向量,根据线面角列方程计算
的法向量,根据线面角列方程计算![]() 的值即可得出结论.
的值即可得出结论.
(1)证明:由题意可知A1D=1,A1E=2,∠DAE=60°,
∴DE![]() ,
,
∴A1D2+DE2=A1E2,∴A1D⊥DE,
∵二面角A1﹣DE﹣B成直二面角,即平面A1DE⊥平面BDE,平面A1DE∩平面BDE=DE,
∴A1D⊥平面BCED.
(2)由(1)可知DE⊥BD,
以D为原点,以DB,DE,DA1为坐标轴建立空间坐标系D﹣xyz,如图所示,
则D(0,0,0),B(2,0,0),A1(0,0,1),C(![]() ,
,![]() ,0),
,0),
则![]() (
(![]() ,
,![]() ,0),
,0),![]() (2,0,0),令
(2,0,0),令![]() (0<λ<1),
(0<λ<1),
则![]() (2
(2![]() λ,
λ,![]() λ,0),即P(2
λ,0),即P(2![]() λ,
λ,![]() λ,0),
λ,0),
∴![]() (2
(2![]() λ,
λ,![]() λ,﹣1),
λ,﹣1),
由(1)知![]() (0,1,0)为平面A1BD的一个法向量,
(0,1,0)为平面A1BD的一个法向量,
则cos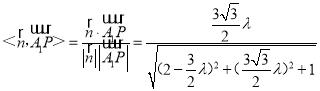 ,
,
令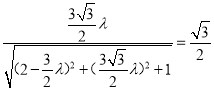 ,解得λ
,解得λ![]() ,即
,即![]() (
(![]() ,
,![]() ,﹣1),
,﹣1),
∴A1P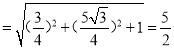 .
.
∴线段BC上存在点P使得直线PA1与平面A1BD所成的角为60°,且A1P![]() .
.


科目:高中数学 来源: 题型:
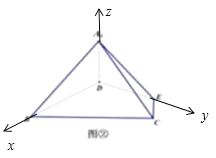
【题目】在三棱锥A﹣BCD中,∠ABC=∠ABD=∠CBD=90°,BC=BD=BA=1,过点A作平面α与BC,BD分别交于P,Q两点,若AB与平面α所成的角为30°,则截面APQ面积的最小值是( )
A.1B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,已知
,已知![]() .
.
(1)令![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足:
满足:![]() .
.
①求数列![]() 的通项公式;
的通项公式;
②是否存在正整数![]() ,使得
,使得![]() 成立?若存在,求出所有
成立?若存在,求出所有![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①,在矩形ABCD中,AB=2,BC=1,E是CD的中点,将三角形ADE沿AE翻折到图②的位置,使得平面AED′⊥平面ABC.
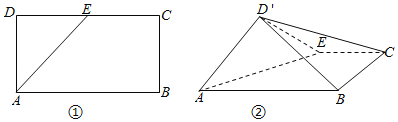
(1)在线段BD'上确定点F,使得CF∥平面AED',并证明;
(2)求△AED'与△BCD'所在平面构成的锐二面角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
如图所示多面体中,AD⊥平面PDC,ABCD为平行四边形,E,F分别为AD,BP的中点,AD=![]() ,AP=
,AP=![]() ,PC=
,PC=![]() .
.
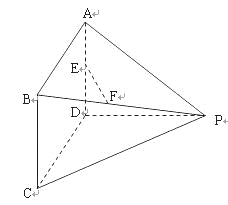
(Ⅰ)求证:EF∥平面PDC;
(Ⅱ)若∠CDP=90°,求证BE⊥DP;
(Ⅲ)若∠CDP=120°,求该多面体的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某校高三年级100名学生的视力情况进行统计(如果两眼视力不同,取较低者统计),得到如图所示的频率分布直方图,已知从这100人中随机抽取1人,其视力在![]() 的概率为
的概率为![]() .
.
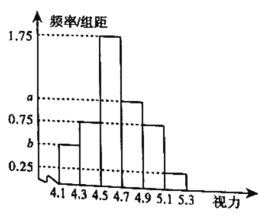
(1)求a,b的值;
(2)若报考高校A专业的资格为:任何一眼裸眼视力不低于5.0,已知在![]() 中有
中有![]() 的学生裸眼视力不低于5.0.现用分层抽样的方法从
的学生裸眼视力不低于5.0.现用分层抽样的方法从![]() 和
和![]() 中抽取4名同学,设这4人中有资格(仅考虑视力)考A专业的人数为随机变量ξ,求ξ的分布列及数学期望.
中抽取4名同学,设这4人中有资格(仅考虑视力)考A专业的人数为随机变量ξ,求ξ的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】支付宝和微信支付是目前市场占有率较高的支付方式,某第三方调研机构对使用这两种支付方式的人数作了对比.从全国随机抽取了100个地区作为研究样本,计算了各个地区样本的使用人数,其频率分布直方图如图.
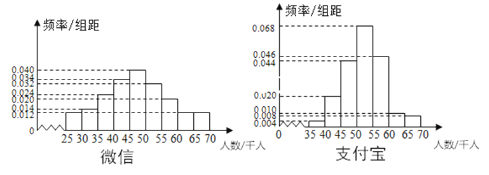
(1)记A表示事件“微信支付人数低于50千人”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为支付人数与支付方式有关;

(3)根据支付人数的频率分布直方图,对两种支付方式的优劣进行比较.
附:

K2![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A、B、C三个箱子中各装有2个完全相同的球,每个箱子里的球,有一个球标着号码1,另一个球标着号码2.现从A、B、C三个箱子中各摸出1个球.
(Ⅰ)若用数组![]() 中的
中的![]() 分别表示从A、B、C三个箱子中摸出的球的号码,请写出数组
分别表示从A、B、C三个箱子中摸出的球的号码,请写出数组![]() 的所有情形,并回答一共有多少种;
的所有情形,并回答一共有多少种;
(Ⅱ)如果请您猜测摸出的这三个球的号码之和,猜中有奖.那么猜什么数获奖的可能性最大?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() ,
,![]() ,
,![]() 分别是椭圆短轴的上下两个端点,
分别是椭圆短轴的上下两个端点,![]() 是椭圆的左焦点,P是椭圆上异于点
是椭圆的左焦点,P是椭圆上异于点![]() ,
,![]() 的点,若
的点,若![]() 的边长为4的等边三角形.
的边长为4的等边三角形.
![]() 写出椭圆的标准方程;
写出椭圆的标准方程;
![]() 当直线
当直线![]() 的一个方向向量是
的一个方向向量是![]() 时,求以
时,求以![]() 为直径的圆的标准方程;
为直径的圆的标准方程;
![]() 设点R满足:
设点R满足:![]() ,
,![]() ,求证:
,求证:![]() 与
与![]() 的面积之比为定值.
的面积之比为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com