
【题目】设函数f(x)=(x﹣a)2lnx,a∈R
(1)证明:函数f(x)=(x﹣a)2lnx,a∈R的图象恒经过一个定点;
(2)若函数h(x)= ![]() f′(x)在(0,+∞)有定义,且不等式h(x)≤0在(0,+∞)上有解,求实数a的取值范围.
f′(x)在(0,+∞)有定义,且不等式h(x)≤0在(0,+∞)上有解,求实数a的取值范围.
【答案】
(1)解:x=1时,f(1)=0,
故f(x)恒过(1,0)点
(2)解:∵f′(x)=2(x﹣a)lnx+ ![]() ,
,
∴h(x)=2xlnx+x﹣a,(x>0),
若不等式h(x)≤0在(0,+∞)上有解,
则a≥(2xlnx+x)min即可,
令m(x)=2xlnx+x,(x>0),则m′(x)=3+2lnx,
令m′(x)>0,解得:x> ![]() ,令m′(x)<0,解得:0<x<
,令m′(x)<0,解得:0<x< ![]() ,
,
∴m(x)在(0, ![]() )递减,在(
)递减,在( ![]() ,+∞)递增,
,+∞)递增,
∴m(x)min=m( ![]() )=﹣2
)=﹣2 ![]() ,
,
∴a∈[ ![]() ,+∞).
,+∞).
【解析】(1)求出x=1时,f(1)=0,得到函数f(x)恒过(1,0)即可;(2)问题转化为a≥(2xlnx+x)min即可,令m(x)=2xlnx+x,(x>0),根据函数的单调性求出m(x)的最小值,从而求出a的范围.
【考点精析】根据题目的已知条件,利用函数的最大(小)值与导数的相关知识可以得到问题的答案,需要掌握求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】对于函数f(x)给出定义:
设f′(x)是函数y=f(x)的导数,f″(x)是函数f′(x)的导数,若方程f″(x)=0有实数解x0 , 则称点(x0 , f(x0))为函数y=f(x)的“拐点”.
某同学经过探究发现:任何一个三次函数f(x)=ax3+bx2+cx+d(a≠0)都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.给定函数 ![]() ,请你根据上面探究结果,计算
,请你根据上面探究结果,计算![]() = .
= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的长轴长是短轴长的
的长轴长是短轴长的![]() 倍,右焦点为
倍,右焦点为![]() ,点
,点![]() 分别是该椭圆的上、下顶点,点
分别是该椭圆的上、下顶点,点![]() 是直线
是直线![]() 上的一个动点(与
上的一个动点(与![]() 轴交点除外),直线
轴交点除外),直线![]() 交椭圆于另一点
交椭圆于另一点![]() ,记直线
,记直线![]() ,
, ![]() 的斜率分别为
的斜率分别为![]()

(1)当直线![]() 过点
过点![]() 时,求
时,求![]() 的值;
的值;
(2)求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=4,AB=4 ![]() ,∠CDA=120°,点N在线段PB上,且PN=2.
,∠CDA=120°,点N在线段PB上,且PN=2. 
(1)求证:BD⊥PC;
(2)求证:MN∥平面PDC;
(3)求二面角A﹣PC﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
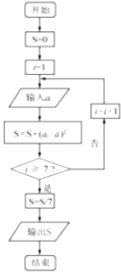
【题目】某人在连续7天的定点投篮的分数统计如下:在上述统计数据的分析中,一部分计算如右图所示的算法流程图(其中 ![]() 是这7个数据的平均数),则输出的S的值是( )
是这7个数据的平均数),则输出的S的值是( )
观测次数i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
观测数据ai | 5 | 6 | 8 | 6 | 8 | 8 | 8 |
A.1
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|2x﹣1|+|2x﹣3|,x∈R.
(1)若函数f(x)=|2x﹣1|+|2x﹣3|的最小值,并求取的最小值时x的取值范围;
(2)若g(x)= ![]() 的定义域为R,求实数m的取值范围.
的定义域为R,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关命题的说法正确的是( )
A. 命题“若![]() ,则
,则![]() ”的逆命题为真命题;
”的逆命题为真命题;
B. 命题“若![]() 或
或![]() ,则
,则![]() ”的否命题为真命题;
”的否命题为真命题;
C. 命题“![]() ”为真命题,则命题p和q均为真命题;
”为真命题,则命题p和q均为真命题;
D. 命题“若![]() ,则
,则![]() ”的逆否命题为假命题.
”的逆否命题为假命题.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是_____________.
①.如果命题“![]() ”与命题“
”与命题“![]() 或
或![]() ”都是真命题,那么命题
”都是真命题,那么命题![]() 一定是真命题.
一定是真命题.
②.命题![]() ,则
,则![]()
③.命题“若![]() ,则
,则![]() ”的否命题是:“若
”的否命题是:“若![]() ,则
,则![]() ”
”
④.特称命题 “![]() ,使
,使![]() ”是真命题.
”是真命题.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com