
分析 (1)f′(x)=$\frac{2x(x+b)-{x}^{2}}{a(x+b)^{2}}$=$\frac{{x}^{2}+2bx}{a(x+b)^{2}}$,可得f′(2)=$\frac{4+4b}{a(2+b)^{2}}$=0,又f(2)=$\frac{4}{a(2+b)}$=2,联立解得a,b.
(2)由(1)可得:f(x)=$\frac{{x}^{2}}{2(x-1)}$,可得4Sn•f($\frac{1}{{a}_{n}}$)=1,化为:2Sn=an-${a}_{n}^{2}$.利用递推关系可得:an-an-1=-1,可得:an=-n.因此证明:-$\frac{1}{{a}_{n+1}}$<ln$\frac{n+1}{n}$<-$\frac{1}{{a}_{n}}$;即证明:$\frac{1}{n+1}$<$ln\frac{n+1}{n}$<$\frac{1}{n}$.令g(x)=ln(x+1)-x,g(0)=0,x∈[0,1].利用导数研究其单调性即可证明:ln(x+1)≤x,令x=$\frac{1}{n}$,则$ln\frac{n+1}{n}$<$\frac{1}{n}$.同理令h(x)=ln(x+1)-$\frac{x}{x+1}$,则h(x)在(0,1)上单调递增.即可证明左边.
(3)bn=-$\frac{1}{{a}_{n}}$=$\frac{1}{n}$,Tn为数列{bn}的前n项和,Tn=1+$\frac{1}{2}$+$\frac{1}{3}$…+$\frac{1}{n}$.由(2)可得:$\frac{1}{n+1}$<$ln\frac{n+1}{n}$<$\frac{1}{n}$.分别取n=1,2,…,2016,右边累加求和可得:ln2017<T2016.左边累加求和可得:T2017-1<ln2017.
解答 (1)解:f′(x)=$\frac{2x(x+b)-{x}^{2}}{a(x+b)^{2}}$=$\frac{{x}^{2}+2bx}{a(x+b)^{2}}$,∴f′(2)=$\frac{4+4b}{a(2+b)^{2}}$=0,又f(2)=$\frac{4}{a(2+b)}$=2,
联立解得b=-1,a=2.
(2)证明:由(1)可得:f(x)=$\frac{{x}^{2}}{2(x-1)}$,∵4Sn•f($\frac{1}{{a}_{n}}$)=1,
∴4Sn•$\frac{1}{2{a}_{n}(1-{a}_{n})}$=1,化为:2Sn=an-${a}_{n}^{2}$.
∴n≥2时,2an=2(Sn-Sn-1)=an-${a}_{n}^{2}$-an-1+${a}_{n-1}^{2}$,
化为:(an+an-1)(an-an-1+1)=0,
∵an+an-1<0,
∴an-an-1=-1,
n=1时,$2{a}_{1}={a}_{1}-{a}_{1}^{2}$,a1<0,解得a1=-1.
∴an=-1-(n-1)=-n.
因此证明:-$\frac{1}{{a}_{n+1}}$<ln$\frac{n+1}{n}$<-$\frac{1}{{a}_{n}}$;即证明:$\frac{1}{n+1}$<$ln\frac{n+1}{n}$<$\frac{1}{n}$.
令g(x)=ln(x+1)-x,g(0)=0,x∈[0,1].
g′(x)=$\frac{1}{1+x}$-1≤0,∴函数g(x)在x∈[0,1]单调递减.
∴g(x)≤g(0),
可得:ln(x+1)≤x,
令x=$\frac{1}{n}$,则$ln\frac{n+1}{n}$<$\frac{1}{n}$.
同理令h(x)=ln(x+1)-$\frac{x}{x+1}$,则h(x)在(0,1)上单调递增.
∴h(x)>h(0)=0.
∴ln(x+1)>$\frac{x}{x+1}$,
令x=$\frac{1}{n}$,则$ln\frac{n+1}{n}$>$\frac{1}{1+n}$.
综上可得:$\frac{1}{n+1}$<$ln\frac{n+1}{n}$<$\frac{1}{n}$.
(3)证明:bn=-$\frac{1}{{a}_{n}}$=$\frac{1}{n}$,Tn为数列{bn}的前n项和,Tn=1+$\frac{1}{2}$+$\frac{1}{3}$…+$\frac{1}{n}$.
由(2)可得:$\frac{1}{n+1}$<$ln\frac{n+1}{n}$<$\frac{1}{n}$.
分别取n=1,2,…,2016,
右边累加求和可得:$ln\frac{2}{1}+ln\frac{3}{2}$+…+$ln\frac{2017}{2016}$<1+$\frac{1}{2}$+…+$\frac{1}{2016}$,
∴ln2017<T2016.
左边累加求和可得:$\frac{1}{2017}+\frac{1}{2016}$+…+$\frac{1}{2}$<$ln\frac{2}{1}+ln\frac{3}{2}$+…+$ln\frac{2017}{2016}$,
∴T2017-1<ln2017.
综上可得:T2017-1<ln2017<T2016.
点评 本题考查了利用导数研究函数的单调性切线方程、数列递推关系、导数函数的运算性质、累加求和方法、不等式的性质,考查了推理能力与计算能力,属于难题.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:高中数学 来源: 题型:解答题
 高三年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
高三年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:| 分组 | 频数 | 频率 |
| [85,95) | ① | ② |
| [95,105) | 0.050 | |
| [105,115) | 0.200 | |
| [115,125) | 12 | 0.300 |
| [125,135) | 0.275 | |
| [135,145) | 4 | ③ |
| [145,155] | 0.050 | |
| 合计 | ④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+2i | B. | 1-2i | C. | 2-i | D. | 2+i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{14}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
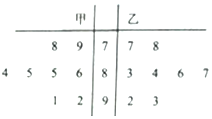 甲、乙两名同学八次数学测试成绩如茎叶图所示,则甲同学成绩的众数与乙同学成绩的中位数依次为( )
甲、乙两名同学八次数学测试成绩如茎叶图所示,则甲同学成绩的众数与乙同学成绩的中位数依次为( )| A. | 85,86 | B. | 85,85 | C. | 86,85 | D. | 86,86 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com