
【题目】已知点![]() ,
,![]() 是抛物线
是抛物线![]() 上的两个动点,
上的两个动点,![]() 是坐标原点,向量
是坐标原点,向量![]() ,
,![]() 满足
满足![]() .设圆
.设圆![]() 的方程为
的方程为![]() .
.
(1)证明线段![]() 是圆
是圆![]() 的直径;
的直径;
(2)当圆![]() 的圆心到直线
的圆心到直线![]() 的距离的最小值为
的距离的最小值为![]() 时,求
时,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图像是由函数
的图像是由函数![]() 的图像经如下变换得到:先将
的图像经如下变换得到:先将![]() 图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图像向右平移
图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图像向右平移![]() 个单位长度.
个单位长度.
(Ⅰ)求函数![]() 的解析式,并求其图像的对称轴方程;
的解析式,并求其图像的对称轴方程;
(Ⅱ)已知关于![]() 的方程
的方程![]() 在
在![]() 内有两个不同的解
内有两个不同的解![]() .
.
(1)求实数m的取值范围;
(2)证明:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
按照某学者的理论,假设一个人生产某产品单件成本为![]() 元,如果他卖出该产品的单价为
元,如果他卖出该产品的单价为![]() 元,则他的满意度为
元,则他的满意度为![]() ;如果他买进该产品的单价为
;如果他买进该产品的单价为![]() 元,则他的满意度为
元,则他的满意度为![]() .如果一个人对两种交易(卖出或买进)的满意度分别为
.如果一个人对两种交易(卖出或买进)的满意度分别为![]() 和
和![]() ,则他对这两种交易的综合满意度为
,则他对这两种交易的综合满意度为![]() .
.
现假设甲生产A、B两种产品的单件成本分别为12元和5元,乙生产A、B两种产品的单件成本分别为3元和20元,设产品A、B的单价分别为![]() 元和
元和![]() 元,甲买进A与卖出B的综合满意度为
元,甲买进A与卖出B的综合满意度为![]() ,乙卖出A与买进B的综合满意度为
,乙卖出A与买进B的综合满意度为![]()
(1)求![]() 和
和![]() 关于
关于![]() 、
、![]() 的表达式;当
的表达式;当![]() 时,求证:
时,求证:![]() =
=![]() ;
;
(2)设![]() ,当
,当![]() 、
、![]() 分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?(3)记(2)中最大的综合满意度为
分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?(3)记(2)中最大的综合满意度为![]() ,试问能否适当选取
,试问能否适当选取![]() 、
、![]() 的值,使得
的值,使得![]() 和
和![]() 同时成立,但等号不同时成立?试说明理由。
同时成立,但等号不同时成立?试说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形,![]() 平面
平面![]() ,
, ![]() 为
为![]() 上一点,
上一点,![]() 为菱形
为菱形![]() 对角线的交点.
对角线的交点.
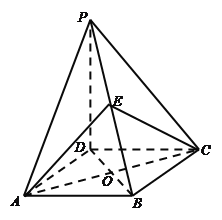
(Ⅰ)证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,四棱锥
,四棱锥![]() 的体积是四棱锥
的体积是四棱锥![]() 的体积的
的体积的![]() ,求二面角
,求二面角![]() 的正切值.
的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() ,且
,且![]() ,②
,②![]() ,且
,且![]() ,③
,③![]() ,且
,且![]() 这三个条件中任选一个,补充在下面问题中,若问题中的
这三个条件中任选一个,补充在下面问题中,若问题中的![]() 存在,求出
存在,求出![]() 和数列
和数列![]() 的通项公式与前
的通项公式与前![]() 项和;若
项和;若![]() 不存在,请说明理由.
不存在,请说明理由.
设![]() 为各项均为正数的数列
为各项均为正数的数列![]() 的前
的前![]() 项和,满足________,是否存在
项和,满足________,是否存在![]() ,使得数列
,使得数列![]() 成为等差数列?
成为等差数列?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正四棱锥P﹣ABCD的底面边长为2,侧棱长为2![]() ,过点A作一个与侧棱PC垂直的平面α,则平面α被此正四棱锥所截的截面面积为_____,平面α将此正四棱锥分成的两部分体积的比值为_____.
,过点A作一个与侧棱PC垂直的平面α,则平面α被此正四棱锥所截的截面面积为_____,平面α将此正四棱锥分成的两部分体积的比值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣sinx,记f(x)的导函数为f'(x).
(1)若h(x)=ax![]() f'(x)是(0,+∞)上的单调递增函数,求实数a的取值范围;
f'(x)是(0,+∞)上的单调递增函数,求实数a的取值范围;
(2)若x∈(0,2π),试判断函数f(x)的极值点个数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图1是某高架桥箱梁的横截面,它由上部路面和下部支撑箱两部分组成.如图2,路面宽度![]() ,下部支撑箱CDEF为等腰梯形(
,下部支撑箱CDEF为等腰梯形(![]() ),且
),且![]() .为了保证承重能力与稳定性,需下部支撑箱的面积为
.为了保证承重能力与稳定性,需下部支撑箱的面积为![]() ,高度为2m且
,高度为2m且![]() ,若路面AB.侧边CF和DE,底部EF的造价分别为4a千元/m,5a千元/m,6a千元/m(a为正常数),
,若路面AB.侧边CF和DE,底部EF的造价分别为4a千元/m,5a千元/m,6a千元/m(a为正常数),![]() .
.

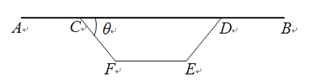
(1)试用θ表示箱梁的总造价y(千元);
(2)试确定cosθ的值,使总造价最低?并求最低总造价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某校组织的一次篮球定点投篮比赛中,两人一对一比赛规则如下:若某人某次投篮命中,则由他继续投篮,否则由对方接替投篮. 现由甲、乙两人进行一对一投篮比赛,甲和乙每次投篮命中的概率分别是![]() ,
,![]() .两人共投篮3次,且第一次由甲开始投篮. 假设每人每次投篮命中与否均互不影响.则3次投篮的人依次是甲、甲、乙的概率___________;
.两人共投篮3次,且第一次由甲开始投篮. 假设每人每次投篮命中与否均互不影响.则3次投篮的人依次是甲、甲、乙的概率___________;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com